The Ethics of Using Computer Algebra Systems (CAS) in High School Mathematics
2010 USACAS and 2012 T3 Conferences
This paper is an adaptation of talks by UCSMP Director Zalman Usiskin on this topic given at the 2010 USACAS and 2012 T3 conferences. The opinions expressed are those of the author.
CAS-capable technology is recommended for UCSMP Algebra classes and for UCSMP Advanced Algebra, FST, and PDM. We strongly believe the availability of this technology enhances student performance in these courses, with additional value for struggling students. Although the displays in this paper are from TI NSpire CAS calculators, UCSMP does not endorse any particular computer algebra system for use with its courses and the arguments here might be applied not only to other CAS equipment but also to other advanced technologies and, in some cases, to any attempts to significantly change an existing curriculum.
The use of computer algebra systems, or "C,A,S" or "CAS" raises ethical questions. Is it ethical for some students to have CAS technology while others don't? Is it ethical to teach students to use CAS on tasks they should be able to do in their heads or easily with paper and pencil? Is it ethical for a student to use CAS without telling the teacher? Is it ethical not to teach some paper-and-pencil algorithms because the task can be done with CAS even though students might later have to know the p-&-p algorithms on a high-stakes test? These are the kinds of questions that this talk is about.
The talk has three parts: First, I define what I mean by ethics and give some examples. Second is a discussion of computer algebra systems in the Common Core Standards in light of these ethics. Last I relate ethics to the use of computer algebra systems in mathematics classrooms.
In fair disclosure, I must warn readers that I have never taken a course in ethics or even a course that has discussed ethics. Thus my look at ethics is not as an academic who is knowledgeable about the field, but as an individual who is trying to sort out the beliefs that people have regarding the use of CAS and other technologies that force one to question what we have been teaching in mathematics classrooms.
Part I: What Do We Mean By Ethics?
Ethics are societal rules of behavior that are based on beliefs. A standard definition is that ethics are the rules or standards governing the conduct of a person or the members of a profession. Ethics contrast with societal rules of behavior that are based on laws or regulations. Of course, many of our laws and regulations can be traced back to ethical considerations, but many of the policies and practices in schools are individual decisions based not on formal beliefs of a profession but on personal beliefs. In fact, it is interesting that we hear often of the ethics of the medical profession or in law or in business but seldom hear of ethics governing the teaching profession.
Yet there are some published ethics relating to teaching. In 1975, the representative assembly of the National Education Association adopted a Code of Ethics of the Education Profession to provide the "aspiration of all educators" and "standards by which to judge conduct". This Code of Ethics is still the ethical law of the land for the NEA. It is in the NEA 2011 handbook and can be seen on the NEA website. Yet it is my experience that only a small percent of teachers know this code exists.
The Code of Ethics has a preamble and two sections. Here is the first paragraph of the preamble.
The educator, believing in the worth and dignity of each human being, recognizes the supreme importance of the pursuit of truth, devotion to excellence, and the nurture of democratic principles. Essential to these goals is the protection of freedom to learn and to teach and the guarantee of equal educational opportunity for all. The educator accepts the responsibility to adhere to the highest ethical standards.
Two sections of the NEA's Code of Ethics follow this preamble. They are separated into a Commitment to the Student and a Commitment to the Profession. It's the commitment to the student that concerns us here. Here is how the Commitment to the Student starts.
The educator strives to help each student realize his or her potential as a worthy and effective member of society. The educator therefore works to stimulate the spirit of inquiry, the acquisition of knowledge and understanding, and the thoughtful formulation of worthy goals.
Is there anything in this statement that bothers you? Is there anything in this statement that might bother some colleagues of yours? I think there is. There are people who do not want the student to inquire or question, and who believe that we, not our students, should set the goals. They believe students should follow the saying "Ours is not to reason why; ours is just to do or die."
This saying is based on two lines in Tennyson's The Charge of the Light Brigade. Here are the first two verses; there are six in all (complete poem).
Half a league, half a league,
Half a league onward,
All in the valley of Death
Rode the six hundred.
"Forward, the Light Brigade!
"Charge for the guns!" he said:
Into the valley of Death
Rode the six hundred.
"Forward, the Light Brigade!"
Was there a man dismay'd?
Not tho' the soldier knew
Someone had blunder'd:
Theirs not to make reply,
Theirs not to reason why,
Theirs but to do and die:
Into the valley of Death
Rode the six hundred.
It's interesting to me that the saying "Ours is not to reason why; ours is just to do or die." Is often viewed as good wisdom for soldiers in battle, while Tennyson meant it in just the opposite way.
The NEA Code of Ethics Commitment to the Student goes on.
In fulfillment of the obligation to the student, the educator--
- Shall not unreasonably restrain the student from independent action in the pursuit of learning.
- Shall not unreasonably deny the student's access to varying points of view.
- Shall not deliberately suppress or distort subject matter relevant to the student's progress.
- Shall make reasonable effort to protect the student from conditions harmful to learning or to health and safety.
- Shall not intentionally expose the student to embarrassment or disparagement.
- Shall not on the basis of race, color, creed, sex, national origin, marital status, political or religious beliefs, family, social or cultural background, or sexual orientation, unfairly--
- Exclude any student from participation in any program
- Deny benefits to any student
- Grant any advantage to any student.
- Shall not use professional relationships with students for private advantage.
- Shall not disclose information about students obtained in the course of professional service unless disclosure serves a compelling professional purpose or is required by law.
These last two statements do not concern the classroom directly, so I will focus only on the first six statements, taking them one at a time.
I call the first of these commitments assuring to the student personal choice and individual liberty. Right off the bat, adhering to this ethic presents difficulties. Beyond a certain age, a student should be able to make decisions for himself or herself regarding what he or she would like to do. But what age is the right age? Some parents allow their children to make decisions regarding bedtime or what their children should eat or when they should study when the children are quite young; others hold off until later years and some parents keep the reins on until a child leaves home. Teachers at all grade levels are faced with continual decisions regarding when all students should act alike and when they should be allowed differences. If we have taught a certain procedure to solve a type of problem, such as a system of equations, and a student uses a different procedure, do we give full credit? Do we give any credit?
With regard to technology in general, should young children be allowed to make a decision regarding what technology to use in doing a mathematics problem? If not, at what age should a child be able to make those decisions? In this regard, I am astonished that some colleges still make decisions regarding what technology students should be allowed to use — at college age I feel a student should make the decision. Yet some colleges don't allow technology. So we see right off that ethics raise fundamental issues with regard to CAS technology or any other technology for that matter.
The second principle is openness. It is in my mind a lemma to the first. Remember that a lemma is a theorem, usually an unimportant theorem that one proves first in order to prove a more important theorem. In this case, a student cannot make choices if the choices are not made apparent to the student. So there has to be openness in order to assure personal choice and individual liberty. There is an obvious application to CAS technology: all students should be exposed to this technology as a different way of doing mathematics; otherwise how can they make a choice?
In this regard, many opponents of using CAS technology — in fact, opponents of almost all use of calculators and computers — view technology as they view adult movies. They do not want children to know of the behaviors that are pictured because they are afraid the children will try to emulate them. Even though using a calculator would not seem to have the life-altering possibilities that having sex at a young age presents, the rules against the use of technology in some places are quite similar. Perhaps I am stretching the point to compare rules regarding the use of technology with sexual behavior. Perhaps a better comparison is with learning to drive. As with cars, there is a notion that children cannot be trusted to use technology wisely; they will use it when it is unnecessary and otherwise improperly. So we should keep the technology from them.
We have slipped into the third ethic, the accurate representation of knowledge. In mathematics, accuracy is an important consideration. The 6th of 8 standards of mathematical practice in the Common Core State Standards is "Attend to Precision". But the accuracy I am speaking of here is a concept that applies to all subjects, namely, to present the subject in a way that is true to the subject. The most blatant examples of inaccuracy in some schools in the United States today occur when biology is taught as if evolution has never occurred or history is taught with the notion that the world less than 10,000 years old or that all history is American history. But some examples of inaccuracy in subjects are far more subtle. When I went to school, virtually all literature we studied was originally written in English. It was as if no other languages had a literature. The few other pieces of literature that were mentioned, such as War and Peace or Don Quixote, were from European languages. It was as if there was no culture to be found in Asia or Africa or South America.
Moving to mathematics, is it an accurate representation of mathematics to teach algebra without CAS technology? Suppose we were to have an algebra class in which we did not allow students to use paper and pencil, in which every problem had to be done in one's head. We would be dishonest to our subject, not just because so much of algebra is done with algorithms that require writing instruments, but because there are those who believe, as David Hilbert did, that mathematics is essentially the work with the symbols we write down. Do away with the written symbols and one does away with mathematics.
If we agree that it would be a distortion of mathematics to teach it without paper and pencil, it is not much of a stretch these days to say that it is a distortion of mathematics to teach it without the available electronic technology that so many people use.
But there is a difference. The algorithms that we use in algebra were designed for paper and pencil, or — to be more accurate — for some writing instrument and something to write on. We can see these algorithms, from those we use to solve systems to the simplification of rational expressions. The paper-and-pencil algorithms are transparent. But the algorithms that are used in CAS technology are not transparent. Even if steps in an algorithm are shown in a solution, a user cannot tell how the machine is getting from one step to the next and, in fact, the algorithms used by a programmed machine are not always the same as the algorithms that we might use if we did not have the machine. So we are in a world in which students are taught a procedure, say, to complete the square of a quadratic expression, but if they use a computer algebra system to obtain the needed expression, the machine may have used a different procedure. Are we being dishonest? Should we change the algorithms we teach students when they have CAS technology? There are no easy answers to these questions.
In this third part of the NEA Code, the words "relevant to the student's progress" are significant. If the tests that help to determine a student's future do not allow CAS technology, are we being untrue to the student — dishonest in our representation of mathematics — by using CAS? If the tests do not themselves represent mathematics accurately, are teachers obligated to teach to the test? A "Yes" answer to that question can be justified on the basis of being relevant to a student's progress. This is a particularly significant issue for CAS technology because most placement exams at the freshman college level do not allow CAS, and many do not even allow graphing calculators.
The fourth ethic is the promotion of health and safety. We generally do not associate the study of mathematics with affecting the health or safety of our students. But some people certainly think that a child's brain can be adversely affected by too strong an attachment to technology, be it computer games or calculators. They would argue that it is harmful to learning when technology is used to work out mathematics that can be done by many people with facility using paper and pencil. Others, such as the Stanford mathematician and NPR "math guy" Keith Devlin, have argued that computer games are wonderful vehicles for teaching players the logical and symbolic thinking that is the essence of mathematics (see his book Mathematics Education for a New Era: Video Games as a Medium for Learning. A K Peters. 2011. ISBN 978-1568814315). Recently (February 2012) there was a news report that most people think that devices like the iPad and other app-driven hardware will affect the brain, but they are about evenly split between whether the effect will be positive or negative.
Few critics of the use of technology seem concerned that for generations taught before the existence of calculator or CAS technology, the lack of paper-and-pencil skills was a death warrant for future work in any area that applied mathematics. It could be argued that today's technology is a life preserver for those students.
And there is also the question of the more general health of our students. For centuries, many people have viewed mathematics as a wonderful vehicle for training the brain to think logically despite no evidence to back it up. If mathematics teaches logical thinking, then surely it promotes health. But I cannot discuss this point without remembering what the Harvard mathematician Ed Moise said once at an NCTM meeting. He and I were among four people debating what is the best way to approach geometry — Jim Fey and Harry Lewis were the other two. In the question-and-answer period that followed our remarks, someone asked a general question of the panel: Do you believe that mathematics teaches logical thinking? This is the kind of question that few people want to field in such a forum, but Moise immediately took it on. Because he had written the SMSG Geometry, and a later textbook with Floyd Downs that were very rigorous, I expected his answer to be that mathematics, if taught properly, does teach logical thinking. But he was emphatic that it does not teach logical thinking except within the discipline. He pointed out that some of his best friends were logicians, but when you got them out of their subject matter, he felt they thought no more logically than anyone else! The research backs Moise.
So we see that people who embrace technology often do so because they think technology stimulates the brain, while those who are opposed to technology in schools think that technology is detrimental to the development of the brain. Both views appeal to an ethic that schools should enhance a person's health.
The next item on the code of ethics, exposure to embarrassment or disparagement, we might call bullying. Bullying is another one of those items that would seem to have little to do particularly with mathematics. But, in fact, it was the behavior of my 9th-grade algebra teacher towards his students, his constant attempts to motivate them through embarrassment and criticism, that moved me, at the age of 13, to decide that I wanted to teach mathematics. I saw how this kind of teacher behavior affected my classmates, many of whom were quite good students, and I felt I could do a better job than he, and I would not engage in that kind of behavior.
A teacher does not have to engage in this kind of bullying behavior to make this a significant ethic for us in mathematics. Failure rates in first-year algebra are typically higher than any other school subject. This is embarrassing to many who fail, and one reason it is not embarrassing to all who fail is that a person who fails algebra is typically not alone. It is disparaging to our subject that schools have been so willing to put up with high failure rates.
Many schools and school systems are introducing technology to attack this problem, but they are attacking the delivery system instead of the mathematical work itself. I do not see much hope for improving school algebra for students who are at high risk without introducing technology that can do the manipulations that handicap so many of them. Instead of introducing technology that merely changes the delivery system we need to change how students do the mathematics.
The sixth section of the NEA ethics code, fairness, is probably the one we might most easily associate with ethics, and the most familiar to us. Ingrained in us from the time we are children is the line from the Declaration of Independence that all men are created equal. Fairness covers equity.
But even equity is not as easily dealt with as it might seem. Consider students from two schools, X and Y, who have taken the same courses in high school and then take a college-entrance exam such as the ACT or SAT. Suppose the students from high school X average 15 points higher than those from high school Y, not at all uncommon among two schools chosen at random. The testmakers believe that the exam was fair because all students took the exam under the same conditions. But others might argue that the exam was unfair because all students did not have the same learning conditions and blame the unfairness on the school system or on society more generally.
Schools may try to be equitable but in the process introduce inequities. For instance, a common form of equity is to require all students to take mathematics up to a certain level, often a level that is higher than was required a generation ago. This favors students whose parents have taken the mathematics, if for no other reason than the home environment is more accepting of the higher requirement. It also disfavors students who have trouble learning mathematics and are from low-income families, because it places them in a situation where they may need tutoring they cannot afford. Students who bring CAS machines to their homes are at an advantage if the home has computers and lots of other technology. It is very difficult if not impossible to correct economic realities by school policies alone.
If we consider CAS to be a benefit, then part (b) of the sixth ethic says we cannot deny such a benefit to any student. And if we don't provide CAS to all students, then we have violated parts (a) and (c). So, the fairness ethic says that we cannot go partway, either all students should have CAS or none should have it. And, as we all know, equity is a common argument against the use of any technology — it's too expensive to provide for all students, or for all students to procure, so we cannot assume it is available in a class. Yet, that means that all of the positive ethical arguments are ignored, including the desire to allow students independent action and alternate ways of solving problems, to introduce them to all the ways in which mathematics is done in the 21st century and to make it easier to succeed in algebra and later mathematics.
Another difficulty with this sixth ethic is that it is generally considered important for a teacher to recognize and take into account individual differences among students in abilities, backgrounds, and interests. There is a tug-of-war between recognizing differences and yet dealing in an unbiased way with these differences.
Isn't this why we like mathematics? In mathematics, we deal with a consistent logical system, one in which we cannot deduce contradictions from our postulates. Sadly, the real world is not like this. Ethical principles are postulates of behavior, and ethical postulates often lead to contradictions.
These six ethics have shaped my remarks today. My remarks are also shaped by my experiences as a teacher, as a student, as a developer of mathematics curriculum, as a teacher educator, as a learner. From these things, like many others I believe that people learn best when they can relate what they are learning to prior experiences. We put the new knowledge into an old framework, what you might call a storyboard. My choice of a storyboard for today's talk is the Common Core Standards.
Part II. CAS in the CCSS
Let us analyze how CAS is treated in the Common Core State Standards in relation to these ethics. The first mention of CAS is at the very beginning of the document. The 5th of 8th standards of mathematical practice is Use appropriate tools strategically. Here is the detail.
Mathematically proficient students consider the available tools when solving a mathematical problem. These tools might include pencil and paper, concrete models, a ruler, a protractor, a calculator, a spreadsheet, a computer algebra system, a statistical package, or dynamic geometry software. Proficient students are sufficiently familiar with tools appropriate for their grade or course to make sound decisions about when each of these tools might be helpful, recognizing both the insight to be gained and their limitations.
I think this statement is quite significant, because it places electronic technology and paper and pencil in the same category, as tools for solving a mathematical problem. This is important because many people speak as if paper and pencil is a good tool and technology is a bad tool. There is no such implication in this statement. The standard goes on.
For example, mathematically proficient high school students analyze graphs of functions and solutions generated using a graphing calculator. They detect possible errors by strategically using estimation and other mathematical knowledge. When making mathematical models, they know that technology can enable them to visualize the results of varying assumptions, explore consequences, and compare predictions with data. Mathematically proficient students at various grade levels are able to identify relevant external mathematical resources, such as digital content located on a website, and use them to pose or solve problems. They are able to use technological tools to explore and deepen their understanding of concepts. Key related processes: Problem solving. Key related proficiencies: Strategic competence.
I think all of us would agree that this is a quite nice statement. To me this is a statement about personal liberty, the first of the NEA six ethics. It says that a student ought to be able to make a choice of tools to use, and that a mathematically proficient student is one who makes these choices wisely.
It also is an accurate statement about mathematics, reflecting the variety of ways in which people today do mathematics.
However, on close reading, there is something troubling here. Notice that the technology is never used to DO mathematics, to SOLVE problems, to ANSWER questions. The verbs here are: analyze, detect errors, make models, visualize results, explore consequences, compare predictions, identify resources, explore, deepen understanding. But never actually as the first call in DOING the mathematics.
This 5th standard of mathematical practice relates to many of the other seven standards of mathematical practice. Here is a list of all 8.
- Make sense of problems and persevere in solving them.
- Reason abstractly and quantitatively.
- Construct viable arguments and critique the reasoning of others.
- Model with mathematics.
- Use appropriate tools strategically.
- Attend to precision.
- Look for and make use of structure.
- Look for and express regularity in repeated reasoning.
Notice the word "appropriate" in the 5th standard. It is a word with which you cannot disagree. And so the CCSS are peppered throughout with this word! Notice that the 5th standard could just as easily have been written "Use tools strategically". The fact that the world "appropriate" was used tells us that there was a dispute as to which tools might be the most favored in a given situation. In fact, the word "strategically" is another word with which one cannot disagree — it almost is a synonym for "appropriately". So we know that there really was disagreement here.
The writers could have said "Attend to precision appropriately", but they didn't. You get the idea — there was no controversy about precision. It is nice that in the four other places in the high school standards in which computer algebra systems appear substantively, the word "appropriate" does not appear.
The second appearance of CAS is in the narrative of the algebra standards.
...A spreadsheet or a computer algebra system can be used to experiment with algebraic expressions, perform complicated algebraic manipulations, and understand how algebraic manipulations behave…
This statement is important because it recognizes that CAS technology can actually get answers. It goes beyond the 5th principle for mathematical practice, which doesn't have the technology actually doing mathematics. It follows the teacher ethic of the obligation not to disrupt a student's progress. It is also nice that here we see the use of CAS in understanding mathematics. This is critical in arguments about the use of CAS because those against the use often claim that paper-and-pencil work enhances understanding — and the tacit implication is that calculator and computer work inhibit understanding.
This general narrative is operationalized in one specific standard.
(Standard A-APR.6) Rewrite simple rational expressions in different forms; write a(x)/b(x) in the form q(x) + r(x)/b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than the degree of b(x), using inspection, long division, or, for the more complicated examples, a computer algebra system.
I'm sure this standard was very carefully crafted and edited so it is worth some examination. "Using inspection" I suspect is another way of stating "in your head" or "mentally". "Long division" refers to a particular paper-and-pencil algorithm. So we have here the traditional trichotomy of ways to get an answer to an algebra problem: you do it either in your head, with paper-and-pencil, or with technology. So we have to turn to the phrase "more complicated examples" to give some guidance as to when we might use technology. Here I imagine the CCS writers did not want to get cornered into some sort of trap by being specific. When is an example "more complicated"? More complicated than what? One guess is that "more complicated" is going to mean "when the degree b(x) is 2 or more". That is, there will be the expectation in books that students can divide a polynomial by a linear expression, but not much more.
To meet this core standard, here is a division that I assume students would be expected to be able to carry out.
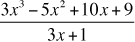
You, the reader, probably learned and remember how to use long division to obtain the quotient q(x) and the remainder r(x). Yet you may not realize that there are two different ways of thinking about the quotient. One way is to think of the quotient as consisting of two polynomials, one that we call the quotient, and the other the remainder. The NSpire functions polyQuotient and polyRemainder automatically give these. This is polynomial division. The Common Core State Standards state the quotient as a rational expression.

The NSpire calculator also has a command, the Expand command, that gives the quotient as a rational expression. Here is what is typed in and what appears when these functions are used.

With such technology, do all students need to have to be able to use paper and pencil to divide polynomials? Most of us in this room deal with mathematics every day, and how often do we have to do these divisions? If very few people need a skill outside of a school and those who encounter the need use technology to obtain an answer, is it worth taking the time to learn it?
I think it is important for students to know that there is an arithmetic of polynomials. They should be able to add, subtract, and multiply polynomials without technology and with, but I question the need for all students to have to be able to use paper and pencil to divide polynomials.
The inclusion of a task like the division of polynomials as a core standard raises the ethical questions of accuracy, recognition of differences, and personal choice. Let us assume that some students need to know how to divide polynomials with paper and pencil. While it may be accurate to represent division of polynomials as so important to mathematics that everyone should learn it, but if it is important, should students not be given a choice regarding how they divide, including the use of technology if they wish? If we recognize individual differences at all, we should recognize that almost all of our citizens have gotten along very well in life and even most of those who have received advanced professional or academic degrees never had to use or even interpret any problem in the division of polynomials. Perhaps even more significantly, when the small percent of people outside of those who teach this content are faced with such a problem, if they use CAS, is it worth taking the time to learn the paper and pencil algorithm? Some skills have become obsolete because of scientific calculators. Shouldn't this skill be obsolete because of CAS?
When I think of something belonging to the core of mathematics about algebra and functions that all high school students should be expected to learn, I think of such ideas as exponential growth, logarithmic growth, direct variation, inverse variation, and inverse square variation. All of these ideas are used by educated people to describe how two quantities are related to each other. That light and sound dissipate as the inverse square of distance, and that population grows exponentially when the growth rate is constant are useful things to know. But I have never encountered a situation outside the mathematical realm where division of polynomials came up.
This is not to say that this is worthless content. It is beautiful stuff, and the behavior of rational functions is quite reasonable material for a precalculus course.
The second division of polynomials changes a rational expression into the sum of a polynomial expression and a rational expression whose end behavior goes to 0. Thus it indicates the end behavior of the original rational expression.

We can see this graphically by graphing the corresponding rational function and the quadratic quotient function. As x increases, the distance between the values of these functions goes to 0. This is also the case as x decreases.
The analogies between division of polynomials and division of integers are powerful. Consider this algebra standard that is not required of all students, described in the Common Core narrative as "additional mathematics that students should learn in order to take advanced mathematics courses such as calculus, advanced statistics, or discrete mathematics":
(Standard A-APR.7) Understand that rational expressions form a system analogous to the rational numbers, closed under addition, subtraction, multiplication, and division by a nonzero rational expression; add, subtract, multiply, and divide rational expressions.
To see the analogy, here is the earlier algebra standard and its arithmetic analogue:
Algebra standard: Rewrite simple rational expressions in different forms; write a(x)/b(x) in the form q(x) + r(x)/b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than the degree of b(x)...
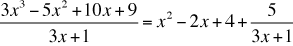
Arithmetic analogue: Rewrite rational numbers in different forms; write a/b in the form q + r/b, where q and r are positive integers and 0 ≤ r < b.
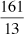 = 12 +
= 12 + 
The polynomial version rewrites a rational expression as the sum of a polynomial and a rational expression that goes to 0 as x increases. The analogue for arithmetic is an integer version changes a fraction into a mixed number, the sum of an integer and a fraction whose value is less than 1. The polynomial version tells us the end behavior of the original rational expression. The arithmetic analogue tells us what might be called the front-end behavior of the original rational number. I chose the fraction 161/13 because it is the value of the rational expression when x = 4. It equals the mixed number 12 5/13. The 12 is a front-end estimate of 161/13; the 5/13 is the error in that estimate. An interesting byproduct of stating this analogy is the realization that as x in the rational expression takes on larger and larger integer values, even though the values in the numerator and denominator increase more and more, the value of the rational expression tends to get closer and closer to an integer.
But this beauty and the applicability of this mathematics has nothing to do with whether you use paper-and-pencil or a calculator to obtain the quotients q(x) or q and the remainders r(x) or r. So one could argue that it is not particularly accurate in our teaching to view the means of obtaining q and r as more important than the result.
Thus I think the Common Core people may have gotten it backwards. The analogy between rational numbers and rational expressions should be for all students, for with technology this analogy is beautiful and can be nicely demonstrated. But the rewriting of rational expressions using polynomial long division should only be for some.
A fourth place in the Common Core Standards where you can find CAS is in the function standards narrative.
Functions presented as expressions can model many important phenomena. Two important families of functions characterized by laws of growth are linear functions, which grow at a constant rate, and exponential functions, which grow at a constant percent rate. Linear functions with a constant term of zero describe proportional relationships. A graphing utility or a computer algebra system can be used to experiment with properties of these functions and their graphs and to build computational models of functions, including recursively defined functions.
This is not the complete narrative about functions; it is only the part of the narrative that deals with modeling. Viewed in this perspective, we see this as a weak statement about CAS, perhaps a very typical statement about when it is appropriate to use technology — not to understand functions or calculate their values, their derivatives, their integrals, not even to use their graphs to determine their behavior — that is, not to disturb the pure mathematics of functions, but only to use CAS when it comes to applications or modeling.
The function narrative anticipates the fifth and last place in the CCS where you can find CAS, in the narrative of the modeling standards.
Graphing utilities, spreadsheets, computer algebra systems, and dynamic geometry software are powerful tools that can be used to model purely mathematical phenomena (e.g., the behavior of polynomials) as well as physical phenomena.
Again we might say that this is a condescending standard. Some people, particularly those who have been opposed to technology use, do not consider modeling to be mathematics. So they are willing to agree to this kind of statement, figuring that when push comes to shove, modeling will not be tested and so will not be in the curriculum. If we think the mathematics of modeling will not be taught, it does not make any difference how it is done.
In toto, what can we make of the Common Core Standards statements regarding CAS? I think most of us would agree that, overall these are nice statements. At face value they indicate that the Common Core Standards support the use of CAS in the classroom. But after some analysis, we see that the statements are not likely to provide much impetus for the use of CAS. But a major thing we can say is that the Common Core Standards do not provide any reason not to use CAS. They sanction the use of CAS. This is an important message: The common core standards expect students to have experience in using computer algebra systems in a variety of ways as they learn about algebra, functions, and modeling.
Part III. Applying Ethics to Answer Some Common Questions about CAS
Given that CAS use is sanctioned, let us consider some common questions regarding its use.
Q1. Is it ethical for a school to provide CAS to some students taking a particular course while others don't have the use of this technology?
To guide us, recall the six NEA ethics that were discussed earlier: (1) assure personal choice (individual liberty), (2) be open, (3) represent knowledge accurately, (4) promote health, (5) do not embarrass or intimidate, and (6) be fair.
Under the fairness ethic, the answer is an unqualified No. Thus, unless a school is trying to study the effects of CAS technology, it would seem to be wrong to have, let's say, an algebra course taught by teachers A and B in which teacher A uses CAS but teacher B does not.
But notice what happens if the situation is modified a little.
Q2. Is it ethical for a school to allow students to make a choice regarding the use of CAS technology by offering sections of a course in which the technology would be used and other sections in which it would not be used?
Now the personal choice ethic comes into play and the answer seems to have changed to an unqualified Yes,
But a student confronted with a choice of different sections needs more information to make a decision. The student needs to know much difference would there be in the two sections. There are two extreme situations: One extreme is that the sections do not differ in content but only in approach to that content. The other extreme is that the use of the technology causes the courses to be substantially different. And there are all sorts of possibilities in between these extremes.
Consider first the situation where the sections do not differ in content but only in approach. If this is implemented, we now have to question why CAS would be used if the content is not changed. We have to question whether this course represents content accurately because the scope and sequence of traditional mathematics courses have been designed around paper-and-pencil skills. Are we portraying the traditional mathematics accurately by using CAS — I would say No. Are we portraying contemporary mathematics accurately with CAS in this situation? I would again say No.
On the other hand, if the use of the technology caused the courses to be radically different, it might be more likely that the portrayal of the mathematics is similar but now it might not be fair for some students to have a section with CAS and other students to have a section without CAS.
Thus, from the standpoint of portraying content accurately, a course in which CAS is used but the content is not changed is not ethical. This is to some extent the situation in which many curriculum developers, including the Common Core standards writers, found themselves. And so they left the standard content relatively unchanged and promoted CAS mainly in content that has little or no curricular history and no rules of the game. So they promoted CAS most with mathematical modeling.
The first two questions have looked at the issue of the use of CAS from the standpoint of school policy. The next question comes from the student perspective rather than the school perspective.
Q3. Is it ethical to allow those students who have access to a CAS to use it knowing that other students do not have such technology?
Here the ethics of fairness and personal choice provide conflicting answers. It is not fair to allow the use of CAS by some but not all students, but it violates personal choice to disallow the use of CAS.
So we see again that ethical principles are not consistent. How do we resolve questions when the ethics conflict? This is a basic question in the study of law, and the answer is that, if there is no specific law to resolve the question, the resolution is done by appealing to precedent. Those who believe that the answer to Question (3) is No will look for precedents that support fairness as the dominating factor. Those who believe that the answer to (3) is Yes will look for personal choice as the determining factor.
I argue that if this were a competition, then fairness would trump personal choice, for in competitions one must go by the rules of the game if one wishes to compete. However, in my opinion learning should not be a competition with others, but a competition within oneself to become better, and under that conception of learning, every student should be allowed to use CAS.
My view of learning is, however, the minority view when it comes to educational policy in this country. The federal government has couched the success of our educational system not in terms of our improvement, but in terms of competition with other countries in the world. Thus, even though on virtually every barometer of mathematics performance, students in the United States have significantly improved over the past two decades, that is, since the NCTM Standards first appeared, the view conveyed by the Department of Education is that we are behind. Indeed, the view is wrongly conveyed that the U.S. is doing worse with respect to other countries than ever before, a view that is not supported by test data.
Within the United States, the same notion of competition is conveyed by publicizing the gap between the average performance of Whites and Asians on the one hand, and Hispanics and Blacks on the other, rather than on pointing out that in all these groups there has been substantial improvement in performance over the past 20 years.
It is a fact that students compete for scholarships, for college entrance, and for jobs. This makes it easy to view the entire educational process as one in which the goal is for you to learn more than your classmates, rather than for you to learn as much as you can, and not worry about your classmates.
From a mathematics point of view, because technology is ignored in the doing of mathematics and mentioned in the applying of mathematics, the Common Core Standards can be viewed as restricting the competition to pure mathematics and not applied mathematics. I think this is because the CCS writers realized that tests would be very likely to emphasize pure mathematics, so they decided to keep the playing field even there and not worry as much about applied mathematics that is unlikely to be tested.
The irony then is that we have students competing to learn tedious methods of doing mathematics, taking precious time away from both theory and application. Furthermore, there are ample precedents that removing the tedium opens up new vistas of mathematics, both pure and applied.
Consider the following historical example. In the late 1500s, the renowned astronomer Tycho Brahe determined the positions of stars and planets in the sky to an accuracy never before obtained. Then, around 1613, using Tycho's measurements, Kepler worked out the orbits of the planets and determined they were ellipses with the Sun at one focus. In doing so, Kepler used logarithms, a mathematical tool that had been invented only 12 years earlier. The use of tables of logarithms enabled Kepler to perform complicated arithmetic with relative ease.
Now imagine if someone said to Kepler, "I'm sorry, Johannes, but you cannot use those tables of logarithms. You have to work the arithmetic using the traditional algorithms. And the reason is that not everyone has access to these tables."
Log tables had been preceded by trig tables. In the 16th through the 19th century, when explorers were going to parts of our planet that had never been mapped, tables of sines and cosines and other trigonometric functions were applied in a manner very similar to the content we teach today in trigonometry, to determine distances and locations that could not be directly measured.
Now suppose someone had decided to ban the use of trig tables, requiring that people find decimal approximations to the values of the trig functions by hand.
The equity argument, which is essentially to wait until everyone has the technology before allowing its use, can be viewed as a perversion that works to hold back those who don't have the technology and, rather than reduce any sort of inequities, enlarges them. The rich — and here I mean "technology-rich" will use these instruments anyway, and to keep them from the poor — and here I mean "technology-poor" means that the poor will lag further behind.
Ironically, our public schools exist because in the 19th century we were concerned that not everyone was getting the education that the upper class was receiving in private schools, and we considered it so important that we allocated public funds to allow all students to receive the best education possible.
Returning to Q3, then, we see that to allow students who have CAS to use it assures personal choice, is open, and represents the latest in knowledge about our field. Allowing students to use CAS if they have it may or may not promote their ability to perform certain mathematical tasks — that depends on what else is done in the classroom — and can be intimidating to those who do not have CAS. It is not fair to allow CAS for some and not for all, but banning CAS does not remove the inequities; it just hides them.
Q4. Is it ethical for a student to use CAS when a teacher expects paper-and-pencil and without telling the teacher?
A "Yes" answer to Q4 assures personal choice. But is it open? That ethic read that the teacher should not unreasonably deny students access to other points of view. We might argue that for a student to use CAS surreptitiously unreasonably denies the teacher access to the student's point of view. Or we could argue that there is an ethic missing from the NEA's list — honesty, an ethic that should apply to all of us. Or we might just say that using CAS but not telling is unfair. Thus I view Q4 as a relatively simple one; It is not ethical. Students should be required to disclose when they are using CAS or other advanced technologies. An advantage is that disclosure can inform the teacher as to when that advanced technology is viewed by students as reasonable to use.
A related question is a little more difficult.
Q5. Is it ethical to allow students to use CAS on tasks they should be able to do in their heads or easily with paper and pencil?
From the standpoint of personal choice, students should be allowed to use CAS on any task, if they are allowed to use CAS at all. This goes along with the Common Core Standards of teaching students to make wise decisions regarding when to use technology. But there is an obligation to prepare students for later work, and having to resort to outside help of any kind on simple tasks can get in a person's way when doing multi-step problems. Also, the ability to do certain tasks in one's head or quickly with paper-and-pencil provides a way to check results obtained using technology. Mental checking is an important skill for students to have.
We have all been frustrated to receive students who obtain answers to mathematical problems but have no idea whether the answer makes sense or how to check whether the answer makes sense. "How do you know your answer is correct?", we ask the student, and we hear back something of the sort, "I did such and such...". The student's response is unsatisfying, so we repeat, "But how do you know that what you did has given you the correct answer?" Now we hear from the student, "Isn't it correct?". We are frustrated. A student who does not have a way to check an answer that is different from the way that the answer was first obtained is a student who does not know enough. To be able to check work in one's head, or quickly with a few paper-and-pencil steps, even if just with estimates, is an obligation we have to all of our students in preparing them for all later work and life.
So, yes, it is ethical to allow students to use CAS on tasks they should be able to do without any technology, but this comes with a price, namely that total dependence on technology is not a virtue.
In reflecting the subject accurately, there is the particular responsibility not to teach something in such a way that it has to be untaught. Some would say this as: Do not teach or even allow bad habits and do not tolerate incorrect understandings. But what is a "bad habit" to one person may not be a bad habit for another, either because the second person may have no option except to do it the "bad" way, or because there may be a difference in opinion as to what is considered "bad" in the first place. Still, we might all agree that a bad habit is to blindly accept answers regardless of how the answers were obtained.
The last question I wish to consider is perhaps the most difficult at the present time.
Q6. Is it ethical not to teach some paper-and-pencil algorithms because the task can be done with CAS even though students might later have to know the paper-and-pencil algorithms on a high-stakes test?
Suppose we decide that teaching long division of polynomials with paper-and-pencil is a waste of time. Instead we show students how to replace 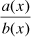 by
by 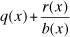 using technology, and we show students how to check this work with the same technology. And suppose we have made this decision partly because we want also to avoid having to teach long division in arithmetic, feeling that we can possibly save months of work in elementary school by not expecting paper-and-pencil competence and again showing students how to obtain answers to division problems and how to check them.
using technology, and we show students how to check this work with the same technology. And suppose we have made this decision partly because we want also to avoid having to teach long division in arithmetic, feeling that we can possibly save months of work in elementary school by not expecting paper-and-pencil competence and again showing students how to obtain answers to division problems and how to check them.
This accurately represents mathematics today in the sense that division of numbers is, in practice, far more often done by calculators than by hand and division of polynomials is rarely done by any means. But it goes up against quite a number of other ethics beyond the obvious obligation of preparing students for places that might not allow technology. It can be unfair, placing students at a disadvantage in college placement tests or the courses of individual professors who eschew technology. Also, not teaching some paper-and-pencil algorithms takes away personal choice regarding how to obtain an answer. It also does not recognize that paper-and-pencil algorithms can be instructive.
Thus, avoiding some paper-and-pencil algorithms completely runs counter to a number of ethics. It suggests that, in the current times when there are still many places where paper-and-pencil competence is needed in high-stakes situations, at a minimum, students be exposed to some paper-and-pencil way of obtaining the answers to questions. The exposure should be long enough to be able to do simple problems by hand. The question still remains as to what is a "simple" problem, and here many schools typically recognize that there are differences among students and what is a simple problem for a better student may not be a simple problem for a poorer student.
Summary
In this talk, I have noted that in mathematics, we choose our postulates carefully so that they are consistent. As a result, we cannot obtain conflicting conclusions from the same given information. But ethical principles do not possess these traits. Examining questions regarding the use of CAS from an ethical perspective has not given me definitive answers to the use of CAS in various situations, but has helped me better understand why people differ in their conclusions about its use. It has also gotten me to realize that some questions and policies about what we do in the classroom are as much ethical questions as they are questions about curriculum and instruction. I hope it has done the same for you.
Contact
UCSMP
1427 East 60th Street
Chicago, IL 60637
T: 773-702-1130
F: 773-834-4665
ucsmp@uchicago.edu