The Importance of the Transition Years, Grades 7–10, in School Mathematics
Adapted from talks presented by UCSMP Director Zalman Usiskin at the meetings of the NCSM, NCTM, and the Metropolitan Mathematics Club of Chicago in April and May 2004.
The mathematics of grades 7–10 has a special character. That is easy to say because every level of mathematics has its own special character. But I am going to argue for a view that I know I would not have argued twenty years ago, because I could not have argued it then. I wish to assert that the particular developments in mathematical thinking that take place in grades 7–10, or perhaps 6–9, or perhaps 6–10—or should take place in those grades—constitute the most important set of developments in a person's mathematical schooling.
The 12-year-old who enters 7th grade is a baby, mathematically speaking. But that same person four years later, upon entering 11th grade, is expected to be acquainted with many o f the most important mathematical ideas that exist. In that four-year span, the successful student has traversed at least seven important transitions:
- from whole number to real number;
- from number to variable;
- from properties of individual figures to general properties of classes of figures;
- from inductive arguments to deductive ones;
- from operations on two numbers to statistics with sets of numbers;
- from informal description to formal definition of mathematical ideas; and, overall,
- from a view of mathematics as a set of memo rized facts to seeing mathematics as interrelated ideas accessible through a variety of means.
I think it is accurate to say that for most students in our country, these transitions are not made. There is mathematics taught, but that mathematics does not deal with these transitions. We view mathematics as either elementary school mathematics, or high school mathematics. In grades 7 and 8 in most schools in this country, and to a lesser extent in grade 6, we remediate slower students with elementary school mathematics and we accelerate the faster students with high school mathematics. And for the majority, we consolidate what they have learned. In some schools, even schools using the most up-to-date materials, the special character of middle-school mathematics is not mathematical, but pedagogical. Teachers use group work, projects, and explorations, but they do not give attention to the above transitions.
And then when students get to high school, even the pedagogy is lost. Teachers assume their students have made many of these transitions and, since the students have not made the transitions, they are obliged to memorize their way through algebra and geometry and functions. They are asked to think formally but they do not know what this means. They are assumed to understand the properties of real numbers, but they are still thinking in terms of whole numbers. They can substitute numbers for variables and they can solve some equations, but they still don't feel that algebra does anything that arithmetic did not do.
The remainder of my remarks explain these mathematical transitions.
Transition 1: From whole number to real number
The transition from whole number to real number has three major steps: from whole number to fraction, from fraction to rational number, and from rational number to real number.
For the first transition, a teacher needs a deep understanding of “fraction”. What is a fraction? Is 2/3 (with a slash) a fraction? Is 12/5 (numerator bigger than denominator) a fraction? Is 6 2/5 (a mixed number) a fraction? Is 2.4 a fraction? Is -2.4 a fraction? Is 1776 a fraction? Is 50/5 a fraction? Are 0.72 or 72% fractions? Is π/2 a fraction? These questions can lead to very interesting discussions among teachers. People do not agree on the answers, for good reason. There are at least three different meanings of "fraction”.
First, 2/3, 12/5, 50/5, and π/2 are fractions in the mathematical sense, for they represent a number as a quotient and use a symbol for fraction. Second, all the above numbers except 1776 and 50/5 are fractions in the everyday sense of being numbers that are not integers, but that is a different notion of "fraction" than the notion of a fraction as a quotient. Only 2/3, 0.72 and 72% are fractions in a third sense, namely, as numbers between 0 and 1. Part of what we have to do with our students is to point out these three different meanings of fractions because most of us use all three meanings and may not even realize it, and students, as you might expect, become confused.
Some people treat rational number and fraction as synonymous, which I think is a bad practice because it does not recognize the difference between the symbol and the number it represents. Students so easily believe that √4 is irrational be cause they are swayed by the radical sign. The examples of π/2 and 1776 should be enough to indicate the difference: π/2 is not rational but is a fraction; 1776 is rational but not a fraction. Of course, π/2 may not be a good example to use because it is not very well understood by students either.
The transition to rational number also requires dealing with operations. What does it mean to multiply or divide fractions? Clearly multiplication must be more than repeated addition and division more than repeated subtraction. Area models, rate factor models, and size change models are needed for multiplication; rate and ratio models are needed for division.
To move from rational number to real number requires an understanding of infinite decimals. We see the lack of understanding when students do not see π or √4 as single numbers or as "definite" numbers.
Here is a sequence that can help students to understand the idea. First is to recognize that an infinite decimal can be considered as a sum of infinitely many numbers. For instance, the infinite decimal 3.14159... for it can be considered as the sum of 3, .1, .04, .001, .0005, .00009, etc., or as the sum of 3, 1110, 4/100,1/1000, 5110000,9/100000, etc.
But how can a sum of infinitely many numbers be a finite number? For this, we need simpler examples. Perhaps the easiest is to consider the infinite sum of reciprocals of powers of 2:
1/2 + 1/4 + 1/8 + 1/16 + ...
We can view this sum geometrically. Think of dividing a square into two, then dividing half of it into two, then dividing the smallest half into two, and so on.
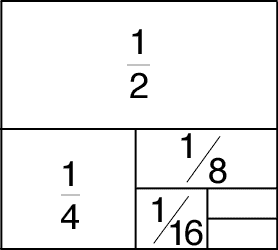
Fig. 1
This gives us
1 = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ...
We can repeat this example using decimals. The result is
1 = .5 + .25 + .125 + .0625 + .03125 + ...,
which again presents an infinite sum on the right and a finite value on the left.
However, suppose that we do not know the finite value on he left and we have a sum of infinitely many numbers on the right. Since it is easy to make up an sum of infinitely many numbers that is infinite, we need some process by which we can determine when the sum is finite. The mathematical theory is the theory of limits, but the idea is easy enough to be introduced in grades 7–10. We use the same example:
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ...
Now we need to view the sum of infinitely many numbers in a different way, as a limit of sums of finitely many numbers. We begin with the first, then add the first two, then the first three, then the first four, and so on, and we look for a pattern. You are familiar with what happens.
1/2
1/2 + 1/4 = 3/4
1/2 + 1/4 + 1/8 = 7/8
1/2 + 1/4 + 1/8 + 1/16 = 15/16
1/2 + 1/4 + 1/8 + 1/16 + 1/32 = 31/32
Now we set up the sequence of sums: 1/2, 3/4, 7/8, 15/16, 31/32, ... and ask what number they are getting closer and closer to. That number is 1, which we call both the limit of the sequence and the value of the infinite sum.
To calculate successive decimal places in an infinite decimal like that for π, we use a third way of approaching real numbers, through nested intervals. The number π is the circumference of a circle with diameter 1. We approximate it from below by the perimeter pn of an inscribed regular n-gon and from above by the perimeter Pn of a circumscribed regular n-gon. So π lies in the interval with endpoints pn and Pn. As we increase n, the difference between these perimeters becomes closer and closer to 0. The real number π is the unique number that lies in this sequence of nested intervals.
I realize that I am not showing you anything that you don't know. What I am asserting is that students in grades 7–10 usually do not see a careful development of this idea. The first time they may see it is in second-year algebra together with the discussion of infinite geometric series. That is too late. Think of the number of students who refuse to believe that the infinite decimal 0.99999... is equal to 1 because they want to put a number to the right of the three dots.
Transition 2: From number to variable
There are many transitions from number to variable because there are a number of different uses of variable. The use of a variable as an unknown is different from its use as a pattern generalizer, or as an argument or parameter in a function, or as a placeholder. The example on the next page involves two of these uses, first as a pattern generalizer, then as an unknown.
Question: Consider the following instances of a pattern:
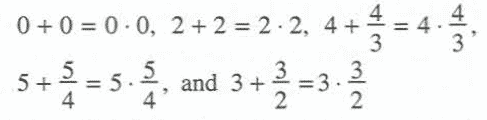
Which generalization below captures the essence of the pattern?

Solution: If choice (1) were the essence of the pattern, then the pattern would be asserting that adding a number to itself is the same as multiplying the same number by itself. This is true for the first two instances but not for the others. But clearly the numbers added and multiplied have been rather carefully chosen. Choice (2) does generalize the instances, since the instance 0 + 0 = 0 · 0 can be rewritten as 0 + (0/5) = 0 + (0/17) and 2 + 2 = 2 · 2 can be rewritten as 2 + (2/1) = 2 * (2/1). Choice (3) is even better for it recognizes that the same numbers are on both sides. But there is much more to this pattern, for the two numbers a and b in choice (3) are related. Specifically, in each instance, we can describe the second number as a quotient in which the denominator b is one less than the numerator a. For this reason, although (2), (3), and (4) all are accurate descriptions of the pattern of these instances, (4) is the only description that captures the full essence of the pattern. The description
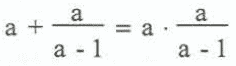
covers all five instances. Furthermore, algebraic manipulation shows the left side equals the right side for every value of a but the number 1. But does this description capture the true essence of the description? Could there be a value for b other than a-1? Suppose
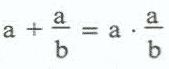
First we multiply by b, which cannot be zero since it was in the denominator.
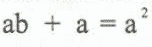
Now subtract a from both sides and factor the right side.
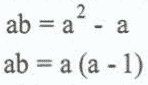
To find b, we have to divide both sides by a. But we cannot do that if a = 0. So there are two possibilities:
either a = 0 or b = a - 1.
That is, when the sum of two numbers equals their product, either the first is 0 or the second number is the quotient of the first number and one less than that number. And when we look at the first instance in the pattern, we realize that 0 ÷ 0 = 0 * 0 could represent 0 + (0/b) = 0 * (0/b). So if a = 0, then b can be any number. Otherwise, b has to equal one less than a.
Is 3 + 1.5 = 3 · 1.5 an instance of this pattern? Yes, if a fraction is thought of as a performed quotient, since 1.5 = 3/2. No, if a fraction is thought of as an indicated quotient.
Once the students understand this use of algebra, we can ask if there are any times when the difference of two numbers equals their product, or their quotient, and so on.
Usually when we give a pattern, the pattern is so obvious that students do not get an opportunity to examine their notion of variable. They just think that a variable takes the place of a number. In order to understand the notion of variable as pattern generalizer, one has to examine what is meant by a generalization and examine when the generalization holds and when it doesn't. It means never forgetting what the generalization is generalizing. Moving back and forth between instances and generalizations is critical.
Transition 3: From properties of individual figures to general properties of classes of figures
Transition 4: From inductive to deductive arguments
The next example tries to handle these two transitions at once. Miss Smith wishes to convince her students that the sum of the measures of the angles of a triangle is 180°. She asks all the students in her class to do the following standard activity.
Activity 1: Draw any triangle on a sheet of paper, measure its angles, and add the measures.
As students finish, they put their sums on the board. Most of the sums are near 180°, but a couple are much less and a few are much greater. After some discussion, Miss Smith summarizes the lesson: "Those of you who got sums that were not near 180° probably read the wrong numbers off of your protractors. If you got a sum near 180°, but not exactly 180°, it is probably because of measurement error. If all our measurements were precise, everyone should get 180°. It is always true that the sum is 180°."
But the data collected by the students do not agree with what Miss Smith has said. Some students are beginning to wonder whether the sum is really always 180. Maybe Miss Smith is oversimplifying, just as is done with grammar rules such as "i before e except after c", being that there are exceptions such as height and weight, not all of them weird. Maybe the sums of angle measures round to 180°. Maybe the sum is 180° only for triangles within a certain range of shapes. Maybe the average sum is 180°.
Furthermore, Miss Smith herself is wondering how to proceed because one of the points she wants to make is that you cannot make a generalization for infinitely many objects just by looking at specific examples. And she also knows that you can never measure exactly. Activity 1 seems like a perfect hands-on activity but it has failed to do what she wants.
The difficulty is that the strategy used by Mis Smith is fine for asserting the truth of m∠A + m∠B + m∠C = 180 for a particular ΔABC, and even for many particular triangles, but not for all triangles. A dynamic geometry drawing program such as Cabri Geometrie or Geometer's Sketchpad does not do it either; Paul Goldenberg has reported that many students think the computer is pre-programmed to get the results it shows.
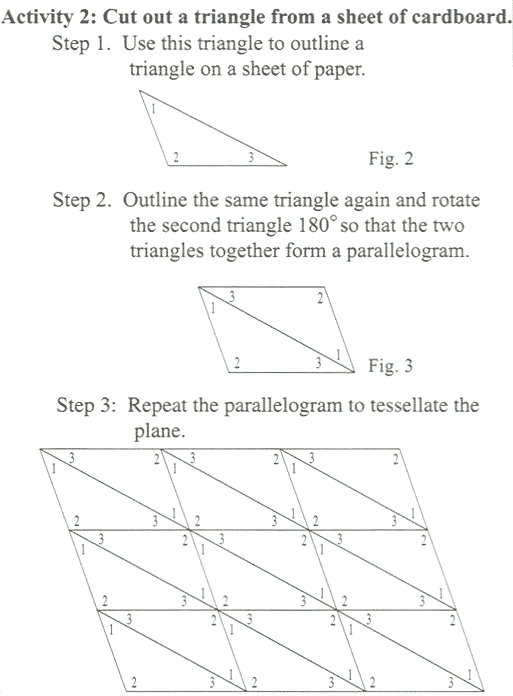
Fig. 4
To show that the angle-sum is 180° for all triangles, some sort of deductive strategy is needed. For a deductive strategy to work, students must understand something that is more basic and then reason from that knowledge. Having such a repertoire of explanations is not easy, because the deduction that convinces a student may not be the same as the deduction one might use in a proof-oriented geometry course. Activity 2 provides an example of an activity that helps the transition from induction to deduction.
When the parallelogram is tessellated, around each vertex are six angles, two copies of each angle of the original triangle. Since the sum of the measures of the six angles is 360°, the sum of three different angle measures is 180°. Now we see that the sum is 180° because it is half of the number 360° that is used for a complete revolution. We should tell our students why the Babylonians chose 360°. We might even tell our students that angle measure does not have to be in degrees. If another unit were used, then the sum would be different.
Notice how Activity 2 uses deduction to transition from studying an individual triangle to an argument that holds for any triangle.
Transition 5: From operations on two numbers to statistics with sets of numbers
Transition 7: From a view of mathematics as a set of memorized facts to seeing mathematics as interrelated ideas accessible through a variety of means
The next example also involves two transitions. This example is from statistics and begins with a comic strip.

The numbers 9.9 and 9.2 in the first strip are statistics; in fact, they are means. (If 10 men were polled and they had 99 close friends among them, then the average number of close friends per man is 9.9.) To us the fraction 9.2 is a joke, a common joke when a mean of counts is not a whole number. But to many people, a fraction indicates the lack of reality of mathematics. Just as you cannot have a "point-two" friend, you cannot trust statistics. And if students have not made the transition from whole number to rational number, they will have great difficulty getting this joke.
The understanding that seems to be lacking here in many people is the notion that in the process of gaining simplicity by using a single number to describe a set of numbers, something is always lost. Here we have single numbers describing entire distributions, and we have lost the distributions.
When I saw these comic strips (following page), I became intrigued. Assuming the same number of men and women participated in the poll, how can you get 9.5 as an average of 9.9 and 9.2? I felt that I ought to be able to answer this question in some mathematically accurate way. Here is my analysis.
The numbers 9.9, 9.2, and 9.5 are rounded to the nearest tenth. Each number stands for an interval. If m and w are the values for the average number of close friends a man and woman have, then 9.85 ≤ m < 9.95 and 9.15 ≤ w < 9.25. (I am assuming we are rounding up decimals that end in 5.) Within these intervals we wish to know whether it is possible to have 9.45 ≤ (m + w)/2 < 9.55, or, equivalently, 18.9 ≤ m + w < 19.1. So one way to answer the question is to give values of m and w that satisfy the three inequalities. You may be able to find such values, but it seems like a very difficult problem to find all possible values.
Unless you graph. Then algebra, geometry, and statistics come together in a beautiful way. The graph of 9.85 ≤ m < 9.95 is a vertical stripe (see Fig.5); the graph of 9.15 ≤ w < 9.25 is a horizontal stripe, and the graph of 18.9 ≤ m + w < 19.1 is an oblique stripe between the lines m + w = 18.9 and m + w = 19.1. And all stripes contain their lower boundaries but not their upper boundaries. The values of m and w that satisfy all three inequalities provide ordered pairs (m,w) that are either on or in an isoceles right triangle. This is hard to see in Fig. 5 so we enlarge the upper right part (see Fig. 6). For instance, one pair of values is 9.88 for m, 9.17 for w, and so m + w = 19.05. So it could have been that the men in the study had, on average, 9.88 friends and the women 9.17 friends. They would have an average of 9.525 friends. And when these numbers are rounded, we get 9.9 friends for men, 9.2 friends for women, and 9.5 for the entire group, just as we wanted. This shows how the power of algebra and the terminology of geometry can aid in understanding statistics.
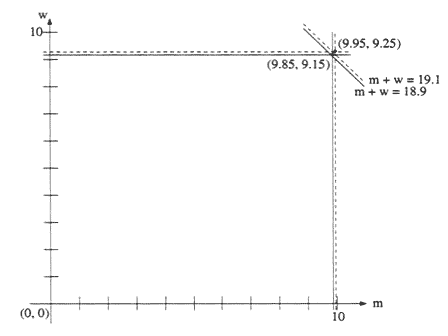
Fig. 5
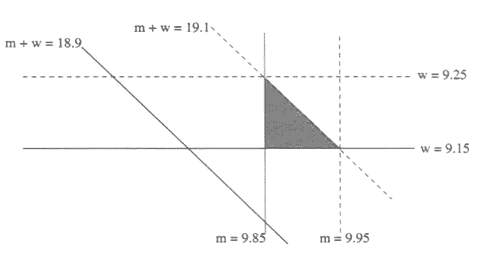
Fig. 6
Transition 6: From informal description to formal definition of mathematical idea
The last example is of the transition from informal description to formal definition of mathematical ideas and has to do with the notion of definition.
The significance of definitions in mathematics is an important transition to be made in grades 7–10. Mathematical definitions are formulated within a mathematical system so that deductions can be made from them. The theorems that are deduced add to our understanding of the idea and can sometimes become alternate definitions for the idea. However, these abstract formulations may not precisely represent the intuitive ideas that created the need for the definition in the first place. Knowledge of the variety of possibilities can assist teachers in knowing why students have trouble both in using their intuition and in applying these abstractions.
Also, definitions in books differ, and the educated teacher needs to know why and what the significance is of these differences. For instance, here are three definitions of rectangle that are currently in high school texts.
- A rectangle is a parallelogram with four right angles.
- A rectangle is a quadrilateral with four right angles.
- A rectangle is a parallelogram with a right angle.
Definition (1), the most commonly used definition in today's geometry books, fits the intuitive idea of a rectangle as a figure with four right angles but it contains more information than is necessary. Definition (2), used in UCSMP Geometry and a few other books, is easiest for students to remember, for it fits the intuitive notion that students have of rectangles. Unlike definition (1), with definition (2) to prove a quadrilateral is a rectangle, you would not need to show that the quadrilateral is a parallelogram. Definition (3) automatically classifies the rectangle and enables us to see immediately that all properties o f all parallelograms apply to rectangles.
If you wished to deduce properties of rectangles, you might want the first definition, because it has so much in it. But if you wanted to show that a figure is a rectangle, you would want either the second or third definitions, because the defining conditions are less stringent. This is a trade-off that often occurs with definitions—the more that is packed into the definition, the easier it may be to deduce properties but the harder it is to find situations where the definition would apply.
While these three definitions of rectangle are all equivalent, many times in school mathematics this is not the case. Different definitions actually classify things differently.
Is 0 a natural number? That depends on your definition of natural number.
Is a parallelogram a trapezoid? That also depends on your definition. In UCSMP, we use the inclusive definition for trapezoid under which a trapezoid is a quadrilateral with at least one pair of parallel sides. We have received more letters from students and teachers about this definition than any other idea we have in our six books. Half of the letters have been sensitive to the fact that we had a choice of definitions and asked why we chose the one we did. But the other half of these letters said flat out that we are wrong to use this definition. Well, we are not wrong. Not only in this particular case does it seem that most mathematicians agree with us, but in general we have a choice of definitions.
Is a rectangle an isosceles trapezoid? It is to many geometers but it is only that way in a handful of books.
Is every rhombus a kite? That depends on the book you have. Some books require that for a figure to be a kite, it must have a pair of adjacent sides of one length and the other two sides of a different length.
Is a line parallel to itself? That depends too on the mathematics book you are using.
The process of examining definitions is more than academic exercise. Throughout school mathematics, definitions of very important ideas change with the domain. Multiplication starts out as repeated addition, but if we stick with this definition, we are stuck when we come to multiplication of fractions. Similarly, powering starts as repeated multiplication, but a different definition is needed when the exponents are not natural numbers. Angles change from being undirected in geometry to being directed in trigonometry. Sines and cosines start as ratios, or as functions of acute angles, and move to functions of real numbers. Congruent figures may start out in elementary school with the classical general Euclidean notion of "same size, same shape" and then move either to definitions restricted to triangles, angles, and segments, or to definitions based on transformations. Are all parabolas similar? To most geometers they all are, but the definition of similarity found in most books does not apply to parabolas.
Each of these moves is difficult for students to make because students have usually been taught there is just one definition for a mathematical term and have to make a major adjustment in their view of a concept when the definition changes. Each of these moves requires that a teacher understand rather deeply the rationales and consequences for the selection of the old and new definitions. Teachers need to study these ideas, but most mathematics teachers are unlikely to encounter any of this material in a mathematics course or workshop not specially designed for this purpose.
Concluding remarks
I have picked only a small part of the enormous range of the curriculum in grades 7–10. There is at least enough material of this kind for two demanding college mathematics courses and years of workshops. These expectations might be appropriate for any person in a secondary mathematics teacher preparation program, and perfect for someone in a middle-school mathematics teacher preparation program, but would only be appropriate for specialists in an elementary education program. Far too many programs do not have room for these kinds of courses.
But there is a greater problem. In grades 7 and 8, teachers were often elementary education majors. It is unrealistic to expect an elementary education major to know enough mathematics to help students make these transitions, yet our curriculum carries those expectations. At the senior high school level, our most experienced teachers tend to teach in grades 11 and 12. And so, in grades 9 and 10 we find the least experienced and often the least qualified of our high school mathematics teachers. As a result, in these years that are so important in the mathematical development of children, the subtleties of the transitions from the hands-on inductive whole number mathematics of arithmetic and individual geometric figures to the symbolic deductive real number mathematics of algebra and classes of geometric figures are not made. My goal in this talk has been to identify the problem in such a way that we can better find solutions to it. We need to encourage colleges and universities to offer courses in the mathematics of these transitions, and not just in the pedagogy. We need to encourage our best teachers to teach at these levels, where the mathematics is so important but students are so often confused by it.
Contact
UCSMP
1427 East 60th Street
Chicago, IL 60637
T: 773-702-1130
F: 773-834-4665
ucsmp@uchicago.edu