• Papers from Conferences
• Applying Arithmetic
• Translations
• Van Hiele Levels & Achievement

The Fundamental Problems in Implementing Curricular Change, and How to Overcome Them

UCSMP Director Zalman Usiskin presented this talk at the opening session of the project's Fourth Annual Users' Conference, held November 5 and 6, 1988. This transcript has been edited slightly for publication.

UCSMP IS NOW FIVE YEARS OLD. In this, our sixth year, we begin the end of the first phase of the project, in which we have developed and evaluated models for curriculum and teacher education, and in general forged the basic plans with which to meet our goals. Now, as we work, we are striving for wider implementation; that work will encompass some of our major efforts in what might be considered the second phase of the project. So I thought it would be an appropriate time to summarize what we have learned about the problems of implementing the changes we feel are necessary to make the needed improvements in school mathematics.

Let us first understand what we consider to be the problems. Huge numbers of students leave school mathematically ill-prepared for the activities they will undertake. They often terminate their study of mathematics too soon, not realizing the importance mathematics has in later schooling and in the marketplace. They do not know enough probability or statistics or applications of mathematics even to be an enlightened citizen. They are not acquainted enough with the current technology to be comfortable with its use in business or in engineering or in the sciences. They are not acquainted with the mathematics used on jobs. And in the mathematics they do take, they do not get enough experience with problems and questions that require some thought before answering, and they do not develop the skills necessary to learn mathematics on their own. As Shirley Hill remarked when she was president of NCTM in 1979, "At the very time we are on the threshold of teaching machines to reason, we are spending an inordinate amount of our educational energies teaching our children mechanistic skills."

UCSMP is the largest university-based project in mathematics education in the country, by far. We receive our funding primarily because others agree with us that these problems are huge and need to be solved. Our largest funding continues to be from the Amoco Foundation, which has given us approximately $6.4 million over the years. Other funders have been and continue to be the Carnegie Corporation of New York, the National Science Foundation, the General Electric Foundation, GTE, and Citicorp. I have the pleasure of announcing here for the first time that UCSMP has received a very large grant, $1.2 million, from the Ford Motor Company, in support of teacher development activities at both the elementary and secondary levels. That funding begins in January of 1989 and will support summer workshops and related activities.

From the inception of UCSMP, one of the principles upon which we have built our conferences is the involvement of school personnel, both as presenters and as participants. Just last weekend the Elementary Teacher Development Component had a meeting of about 60 supervisors from around the country. Some who had never been here previously were surprised at the frankness with which we discuss issues, the opportunities that they had to be involved, and the overall openness with which we handle our activities. Supposedly you who work in schools are in the trenches and we are the ivory tower, but neither you nor we can operate with that kind of metaphor. Henry Adams said, "A teacher affects eternity; he can never tell where his influence stops." We are all teachers, and the world is our trench. As much as our goal is to impart information to you, at our conferences we learn from users where we have erred just as you learn from your students, and we learn from potential users what we must do in order to get our message across. Certain kinds of change constitute our goals; we have received our funding primarily to create programs to institute these changes, and the effort requires input from all parties.

Two Calibers of Change

IT IS CONVENIENT TO DISTINGUISH two calibers of change. If you are thinking of using UCSMP Geometry in place of your regular geometry, or using our Elementary Teacher Development materials to do some in-service of your teachers, or using Kindergarten Everyday Mathematics but not changing first grade as a result, then the kind of change you are thinking of doing requires only that you, and perhaps a couple of others, make a decision and go with it. We encourage this change. We encourage you to use our materials, even piecemeal; we think they are good. Even this caliber of change requires that you be able to answer a number of questions: Why is the change needed? What are the specific problems we are trying to overcome? What makes the new approach better? Is there anything I must do that I haven't done before? Will the students act differently?

The first caliber of change, change of your own behavior or of the behavior of a few colleagues, can be accomplished at a conference like this. Even if you don't like the details of what we do, you may decide that our arguments for change are persuasive and that you must do something. Probably you already have decided; I surely am preaching to some who are already converted.

The second caliber of change is more substantial. It can be distinguished in various ways from the first caliber. Would the change persist if you left your school district? Can the change be so noticeable by someone who receives your students that they must change what they do? This constitutes substantial change. To get substantial change, you must build each year on changes made in the previous year; otherwise even large improvements in one year can decay quickly.

Of the substantial changes that we at UCSMP would like to see, I would like to focus on four, at four different levels.

Primary (K–3). The earliest school experiences, beginning in kindergarten, should exploit real-world experiences and interests of children to develop key mathematics concepts earlier than conventional curricula.

A student completing the kind of elementary program we envision would probably be ready for today's 7th grade mathematics in the 6th grade, having gone through a far richer experience in all the grades preceding.

Elementary (4–6). Beginning at least as early as the 4th grade, mathematics should be taught by teachers whose major responsibility is to teach mathematics.

If music can have a specialized teacher, why not mathematics? A school organized the way we envision would have specialized teachers in science, and perhaps also in social studies, as well as mathematics. Time for mathematics and these other disciplines would be guaranteed by the schedule, and the ability of teachers to maintain subject matter expertise and attend professional meetings would be possible because they would not be pulled by every discipline. The elementary school teacher of today has an impossible job; no one can keep up with knowledge and teaching trends in all the disciplines. Let's realize this and change the position.

Lower Secondary (7–9). The secondary school mathematics experience should begin in 7th grade, with about half of students taking algebra in 8th grade and geometry in 9th.

Average to above average students going through the first four years of the secondary curriculum would complete geometry and advanced algebra by the end of their sophomore year and not be advanced placement students.

Upper Secondary (10–12). All students should have substantial mathematical experiences involving the use of computers to assist in learning and doing mathematics.

Students would then be prepared for all the mathematics they might encounter in college: statistics, computer science, and applied mathematics, as well as calculus.

I have chosen these four ideas not only because they are significant to us, but because they require major changes in the ways in which schools deliver mathematics instruction to children. In particular, a single teacher cannot implement any one of them without help from other teachers and the school administration. As a result, they represent some of the more difficult ideas to implement.

To accomplish this caliber of change, I believe five steps are required.

Step I: Recognize the problem.

THE FIRST PROBLEM in implementing change is that there are always some people who do not believe change is needed. Thus, the first step in implementing change has to be recognition. You must convince people that there is a problem, and if you want major change, you must convince people that there is a major problem.

There is not the time in this talk to detail the problem; instead, I will give you some of the manifestations.

1. At a time when "Sesame Street" counts to 40, many kindergarten books go no higher than 10 or 20. Although channel selectors on TVs go into the 1OOs, first grade books stop at 99. Digital clocks abound, but tend not to be mentioned in primary schoolbooks. Thus, the popular culture contains a huge amount of mathematics, accessible to young children, which schools ignore.

2. By 5th grade, our students are already one year behind their counterparts in Japan and Taiwan. In a 1983 study, in which Jim Stigler from the University of Chicago faculty was involved, only one 5th grader in the United States scored in the top 100 of 720 students from these three countries. A paper by Karen Fuson published just this week in the Journal for Research in Mathematics Education containing an analysis of foreign textbooks, some of which UCSMP translated, found the Soviet and mainland Chinese textbooks similar in grade placement of topics to the Japanese and Taiwanese texts. Thus a substantial part of the world expects far more than we do.

3. On the largest international mathematics study ever undertaken, the Second International Mathematics Study (SIMS), the average Japanese 7th grader scored at the 95th percentile of 8th graders in the United States. All of the 20 or so countries but Japan used 8th graders in this study; the United States scored at the international median in arithmetic, algebra, and statistics, but in the bottom quarter of countries in geometry and measurement. The median is not something to be content with; Nigeria, Swaziland and Thailand, all considered third world countries, were in the sample.

4. By 12th grade the situation is even worse. We keep in mathematics only about 13% of an age cohort and only about 3% of the cohort takes calculus. SIMS concluded that these numbers are "among the lowest of any advanced industrialized country taking part in the Study," and those countries include Belgium, Finland, England, Sweden, Hungary, Canada, as well as Japan and Hong Kong. Only these 13% were tested; still, our algebra achievement was the lowest of any of these countries; only Thailand was lower. As was said about the Olympics, it is not that we in the United States have gotten worse, it is that the other countries have gotten better.

Let me summarize the current situation. If the present curriculum taught in the United States were a new experimental curriculum that we were testing, we would be forced to pronounce it a failure.

If we want any evidence of how important mathematics is, simply take a look at the catalog of any two-year college. It is dominated by high school courses, and not necessarily the upper level courses. You will see many arithmetic and elementary algebra courses. I was told by a major college publisher that the number of intermediate algebra books sold each year at the college level in the U.S. exceeds the number of second-year algebra books sold at the high school level. The problem is there, and it is so large that it almost seems senseless to tackle it. But we must. Mathematics is too important for so large a segment of our population not to be versed in it.

Step 2: Realize you are not alone.

NO ONE WANTS TO BE ALONE in trying to solve a problem. Perhaps the most common thing told to us by school people is, "If we make this major change, what will we do with students who come into the school district from outside?" Think about this question. It assumes districts are alike, which they aren't. Students who come in from other school districts always have to adapt. Students who change from one teacher to the teacher next door have to adapt, often greatly. In switching districts, students may have read a story last year that they will see this year; they may have studied South America last year and find they will study it again. The answer to this question is: every school district has to accommodate students new to it, regardless of its curriculum. Do we refrain from teaching our children reading because some new students who come into the district cannot read as well as ours do? Do we refrain from offering algebra in the 8th grade simply because there are some who are not ready for algebra? No we take pains to get them reading and get them more ready for algebra.

Another answer to the question of what to do with students who are new to the district is to point to the number of organizations that are supporting the kinds of changes we promote in UCSMP: get those reports from NCTM, from NCSM, from MSEB. Make certain that you have reports that are from outside the mathematics community, like "A Nation at Risk" or the reports from the College Board. Otherwise you will be viewed as simply arguing for your own interests. It is important to support the improvements desired by others; science is in worse shape than mathematics, and social studies seems not far behind. A recent study found that a greater percentage of students in Europe could estimate the population of the United States as about 250 million than could those from the United States. How bad must it get before we get specialized teachers in the elementary school? Of all the documents, the most likely to be influential among mathematics teachers and supervisors is the NCTM Standards. We are in very substantial agreement with the Standards, though not on everything. We think more could be done at K–4 than is in the Standards. The 9–12 Standards are unattainable by any but the very lop students unless one begins at grade 8. But the content and the goals of the Standards are very much in line with what we are trying to do. We may disagree in places on the means, but not the ends. The teacher development work we are doing is certainly in line with the Standards, and our secondary curriculum is the only current curriculum in the U.S. in line with them. This is no coincidence; both NCTM and UCSMP are trying to correct the same problems.

Step 3: Explode the myths about change.

THERE ARE MYTHS. 1. The most common myth is that standardized test scores are sure to fall. At the elementary level people are worried about the effects of calculators on the computation tests. At the secondary level, it's the SATs and ACTs.

Our general evidence is that, for the most part, the standardized tests are our friends. Students who are a year ahead will perform a year ahead. The evidence from our evaluations, ranging from kindergarten through algebra, is that this improvement is possible. One suburban school district that adopted Transition Math and Algebra for large numbers of its students in 7th and 8th grades wound up with a school mean of 12.5 on the California Achievement Tests it gave to its 8th graders. The scores were so high that the school sent the tests back to the graders to make certain a mistake had not been made. We expect greater performance on SATs and ACTs with students through our secondary curriculum because many of our students will have had an additional year of mathematics.

But these kinds of substantial improvements can only occur with the second caliber of change. Changes one year must be stepping stones to accomplish changes the next.

2. A second myth is that you either have it or you don't at math, and the purpose of math instruction is to find out who has it. This leads to a practice so common that we take it for granted. When a student is behind, the student is given a slower course. Such students are sorted out, left to believe they can never do it, often put into tracks from which there is no out. There is nothing that such tracking can do except to get them more behind. When a student is behind, we must get into their minds that they need to work harder, not less. They need to catch up. They need to get into the mainstream. And we must find ways for our mainstream students to get into the honors classes. It is a crime that tracking in many high schools is a one-way street; you can go down levels but not up.

How do we destroy this myth, so common in our culture, that math is only for a few? I proceed by analogy. Reading was once thought to be accessible only to the god gifted, the aristocracy. Unless we see something in Arabic or Chinese or Thai, we tend to forget that letters are symbols. Anyone who can learn to read can learn to decode the symbols of mathematics. But we don't teach children or adults to read by giving them lists of words without any context. We teach them with stories and information in context. We know that almost everyone can learn to be literate that way. Now let's get them to be numerate. Giving them lists of multiplications to do won't do it; we need context in mathematics as much as we need it in reading.

At the college level, calculus is used to filter out those who can from those who can't. At a conference last year to discuss how to improve the teaching of calculus, which is considered in as bad shape as any course at any level, one of the participants made the point that calculus is so important in so many endeavors that it should be a pump, not a filter. This became included in the title of the proceedings for the conference. We believe the same could be said for algebra. The failure rate in this country in algebra seems to be about 25%, a disaster given the importance of the subject for all the endeavors one might wish to tackle. Algebra must be a pump, not a filter.

3. The panacea myth. There are myths the other way. Some people think we have all the answers. Some people think UCSMP will cure all your problems. I have had numerous people come up to me and ask something like, "We have been thinking about implementing some of the ideas you propose. What do we do with a student who does not keep up with the others?" Or, "We have an incompetent teacher. What do we do with that teacher?" I have two responses. First is that we cannot solve all the problems of the world of education. There will be students who aren't successful even with the extraordinary materials we have created. There will be teachers who are poor teachers, even after they have been to ten in-service meetings with you in charge. UCSMP is not a panacea; we are only attempting to be a better means to a higher end. My second response is more practical: What do you do now with students who do not keep up? What do you do now with that incompetent teacher? Do not expect your current solutions to become obsolete.

4. A fourth myth is that there is no hope, a belief that nothing can be really be done to change the current situation. The teacher or administrator reads about what is done in Japan and says, "Their society is different. We can't do that here."

HOW DOES ONE CONVEY the needed optimism, the required confidence, the necessary conviction? Look around you. About half of you attending this conference classified yourselves as users of our teacher or student materials. You must think it can be done.

The movement of more material into the curriculum now and earlier has a long history. In Capitalism & Arithmetic: The New Math of the 15th Century, Frank Swetz points out that in the 15th century, our algorithms were unknown. In some schools, students memorized multiplication tables up to 99 x 99 because there was no other simple way to get the answers. Swetz quotes Tobias Dantzig:

There is a story of a German merchant of the fifteenth century, which I have not succeeded in authenticating, but it is so characteristic of the situation then existing that I cannot resist the temptation of telling it. It appears that the merchant had a son whom he desired to give an advanced commercial education. He appealed to a prominent professor of a university for advice as to where he should send his son. The reply was that if the mathematical curriculum of the young man was to be confined to adding and subtracting, he perhaps could obtain the instruction in a German university; but the art of multiplying and dividing, he continued, had been greatly developed in Italy which, in his opinion, was the only country where such advanced instruction could be obtained. (Tobias Dantzig, Number: The Language of Science, New York, Macmillan, 1954, p. 26.)

The first university in the United States to require arithmetic for entrance was Yale in the 1740s.

Expectation is an important variable in education; if we do not have certain expectations for students, they will not achieve them. The best way to insure that something will not be learned is to not teach it.

How does one convince a teacher that there is room in the curriculum for the additional things we want taught? We know of no better start than the Flanders graph. Most of you have seen it before, but it is so important for hope that we must show it again.

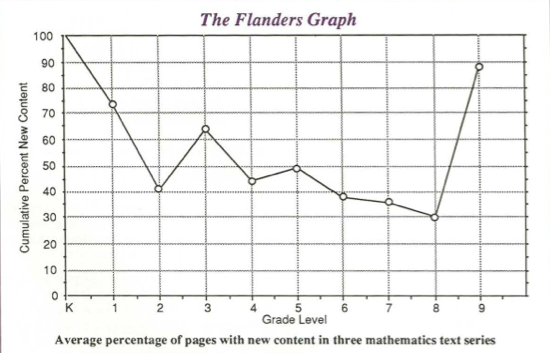
The graph shows where the curriculum can most easily be changed. I've already remarked that at kindergarten and first grade, the curriculum ignores what students know, so we lose time there. At second grade, we lose about a half year alone. There's where we lose to other countries. Karen Fuson concluded from her analysis, which involved textbooks published in 1983 and 1985, that "Both the simplest and the most difficult multi digit addition and subtraction appear earlier (from 1 to 3 years earlier) [in foreign books] than in the United States." I should note that almost all publishers have series that have come out since 1985, and that not all books are alike. You will have to judge the current series for yourself.

We do not lose as much at grades 3–5, but we spend a large amount of time on long division and other complicated paper and pencil computations that many of us feel are obsolete.

We lose at least one more year in grades 6–8, through an inordinate amount of review which often begins, even in 7th and 8th grade, with whole number addition and subtraction. And for those students who have not mastered these skills, having found out what they are bad at, we give them nothing else. They are the crippled and calculators are the crutch, but the tendency is not to let them have calculators. Many schools have the bizarre philosophy: we will not give you calculators until you have convinced us that you do not need them.

Grades 9–12 do not allow time for more. I would guess that geometry would have about a 90% rating in the Flanders scheme of things, second year algebra about 75%, and precalculus about 75%. Even inserting technology does not save time. When one has a calculator or computer that graphs functions, it takes time to learn to use that automatic grapher. Furthermore, since the grapher can do so much more than hand graphing can do, it is natural to take advantage of that extra power to do more than you used to.

Step 4: Articulate with all involved.

PEOPLE MUST TALK. Change of the first caliber does not require much articulation, but change of the second caliber – significant change, multi-year change – requires that administrators and teachers work together. In Illinois, where there are often different elementary and secondary districts in the same community, it can require that two or more districts get together.

Articulation must be both ways, both topdown and bottomup. It must go from administrators to teachers and back. It must go from elementary schools to high schools and back. Teachers cannot make significant change without administrative support, and administrators cannot make significant change without teacher support.

How does one get such a consensus? One thing is to make improvement your goal no one can be against that. Do not necessarily work for UCSMP or any single other specific means of improvement. Look around; what are the best materials? What agrees with the goals of your school or school district? To get people to realize that they need more technology in the schools, bring in business people, if necessary. Would the business community like students to be acquainted with computers? Should students be able to use calculators? Of course.

Now that you've set the stage, you have people to work with you, you have a common purpose, and soon, what do you do? Of course every district is different, but I offer the following suggestions as steps 5 and 6.

Step 5: Be bold but prudent.

THE GREATER THE PROBLEM that is perceived, the greater the changes that people want to make, and the more quickly people want to make those changes. Yet it seems prudent that great changes should be made carefully and slowly. This is an omnipresent paradox in making significant change.

To make major change, have a multi-year plan, but do not change all grades at the same time.

Small improvements can be made in all grades simultaneously. But big change, by definition, cannot. Suppose you wish to make big change in 2nd grade. If you make significant change in 2nd grade, then 3rd grade should be changed next year. If you change 3rd grade at the same time as 2nd, then the 3rd grade students don't have the background needed. You guarantee yourself that this year will be tough, and then next year you have to change third grade again. So it seems more efficient to change one year at a time. It’s also easier to inservice one grade of teacher than all grades.

I say this despite the fact that I reported last year on a school district that changed all six years at once through the adoption of books a year above grade level. That is, the school adopted 2nd grade math books for 1st grade, 3rd grade books for 2nd grade, and so, with 7th grade books being used at 6th grade. The idea was to have one tough year and then all the rest would be easy. It happened that the year wasn't tough at all, except for the beginning of 1st grade. The year was actually quite smooth. So significant change can be done, but I view that district as special. This year the only problem is what to do with students who are new to the district. The teachers notice the difference. My answer: there's review in all elementary school books; some of the review will be new for these students. They will have to work harder, but their parents know this is a district with high standards; that's part of the reason they moved there.

Despite all planning, significant change seldom occurs without some difficulties. There are people who don't understand the changes and unwittingly do things to make the change more difficult, there are more sorts of practices that are based on current norms than realized, and so on – and of course there are the people who were against change from the beginning and look upon everyday problems as having been caused by the new practices.

Anticipate that there may be problems; plan discussions and hand-holding or sharing sessions in advance.

It is important to plan ahead. We have found that, at all levels, teachers do not get enough opportunities to talk about what they do. The initiation of a new practice can be a catalyst to do something that should be done all the time: namely, to get teachers talking with each other about what they teach and how it is going. Frank discussions, chaired by a supervisor or someone designated to have that responsibility, are often better inservices than anyone brought in from the outside.

One benefit of such internal meetings is that decisions can be made so as to anticipate what will happen the next year and correct for anything that may not be going as you would like.

I should note that in many of our components, there are UCSMP staff or other people who have gone to school districts, sometimes many times in the same year and sometimes over a period of years, to assist in inservice. We try to provide as much help as we can.

Of all things that need to be planned in advance, perhaps the most important is a safety valve.

Have a safety valve for students and teachers.

Few if any programs are successful with all students. If a student does not succeed or a teacher does not work out, there needs to be a place for that person. If a new curriculum seems not to have worked in a particular topic area, there must be a plan for what to do the following year. This is still another reason for doing things one year at a time.

Let me illustrate with an example. Suppose you agree with us on the issue of unnecessary review in 6th grade. You decide, therefore, to start books next year at Chapter 4 or 5. The anecdotal evidence is that teachers will be amazed at how much more students learn with this practice. You should not simply take that for granted, however, and you should test in the spring. Suppose it turns out that students do not do as well as the previous year's students did on some topic. The safety valve comes at the end of the school year, or perhaps in 7th grade.

A safety valve is not usually needed. But it is a wise and important thing to have. You need not have the practice spelled out, but always recognize that there is a possibility that things will not occur as you thought.

However, a caution should be stated here. Do not apply safety valves too early. We have had teachers teach from our pilot materials and not appreciate them until the next year, when they had to go back and teach out of their old books. Some people quickly forget how dull it is to give students 50 multiplication or fractions problems two or three nights in a row.

Step 6: Test on the new.

YOU WILL BE REQUIRED to give tests that are biased against new curricula, that are too narrow, or that focus just on paper-and-pencil computation.

This is a fact of life which cannot be avoided. But you must also test on the new things you are trying to accomplish. If you implement calculators, you must test children with them. If you teach geometry at 5th grade, you must test 5th grade children on geometry.

We have had a quandary in evaluating some parts of the project. I f you have truly made significant change, you may find it hard to find a comparison group to determine the magnitude of the change. For instance, suppose you adopt the ideas of our secondary curriculum, and many more students are now taking geometry in 9th grade than did before. You would like to know how much more a student knows now than that same student would have known in your previous setup. You can't compare that student with a l0th grade geometry student because he or she is only a 9th grader. To compare that student with the other 9th graders is very difficult, because if you put a lot of geometry on the test, then the comparison students will become quickly discouraged. The UCSMP students know so much more at that same age that no test designed to show how much more is able to be given to other students.

Some districts have tried to solve this problem by com- paring UCSMP students to the only such high-performing students they know, the ones in their gifted programs. We view that as wrong. We are not trying to make all students gifted. W e are simply trying to give average students the sort of mathematics education they deserve. One cannot expect average students to possess the same inherent desire, ability, and often the home backgrounds that characterize many gifted students.

There are other reasons for testing on the new. It forces teachers to teach the new. And it makes it possible to build each year on the expectations of the previous year.

Final Remarks

AS I FINISHED WRITING THIS TALK, I was struck by the fact that focusing on problems is a depressing thing. The last thing you may have come here for is to hear about problems. Surely you wish to hear about successes and you want to leave here filled with ideas that work.

We are proud of the translations in the International Mathematics Education Resource Center; they have convinced many leaders that change is not only necessary, but possible. We are proud of the curriculum work we have done, both in the primary grades and at the secondary level. Our evaluations have consistently shown some good results, and sometimes dramatically good results. We are proud of our work in teacher development; we feel that only by getting mathematics specialists can we achieve anything close to the kind of curriculum recommended by all the major bodies in mathematics education.

You are probably here because you agree with one or more of our goals. You will find many colleagues here willing to share their thoughts and experiences with you. You will find schools and school districts, some as large as entire cities, some as small as single schools, which have overcome all the problems of implementation, which are doing things that others think difficult or impossible to do.

Users' Conferences in previous years have taught us that many people leave here with a rush, a high that comes from a feeling that you are doing or about to do the kinds of things you have always wanted to do, and from finding that there are others who agree with you both about the problems in mathematics education and the ways to solve those problems. We are very pleased to see so many of you and we hope that you leave feeling that way.

Contact

UCSMP
1427 East 60th Street
Chicago, IL 60637
T: 773-702-1130
F: 773-834-4665
ucsmp@uchicago.edu