A K–12 Mathematics Curriculum with CAS
Presented April 24, 2006
This article is part of a presentation given by UCSMP Director Zalman Usiskin at the Annual Meeting of the National Council of Supervisors of Mathematics in St. Louis, MO, on April 24, 2006. This article was published in UCSMP Newsletter No. 36: Fall 2006-07.
The use of technology has been of interest to me during my entire career. Although my first school achievements in mathematics were partially a result of being exceedingly fast at both mental and paper-and-pencil arithmetic, when the first hand-held calculators appeared in 1971, I was ecstatic. Finally something to take the drudgery out of arithmetic! Two years later, I began work on an algebra text entitled Algebra Through Applications with Probability and Statistics that used calculators. I spoke and wrote on the subject, “What Happens to Arithmetic Now that There Are Calculators?” I felt then and still feel that the elementary school mathematics curriculum will ultimately embrace calculators. Future generations will wonder how anyone could have been against their use.
I first spoke about CAS – computer algebra systems – in a major talk in 1983, at a session at the annual meeting of NCTM that no longer exists: the secondary level general session. I considered being invited to do that session as one of the greatest honors that could be given to someone in mathematics education, and ventured to give a talk that would lay out what I thought should be the high school mathematics curriculum. The title I had chosen a full year before giving the talk was: “We Need Another Revolution in School Mathematics.” I had no idea that, by the time I gave the talk, we would be preparing to start UCSMP, the largest university-based curriculum project since the “new math.”
One of the reasons I gave for the revolution in that 1983 talk was the existence of muMath, a descendant of MACSYMA and the mother of Derive. I thought that muMath would soon appear in a reasonably inexpensive and easy-to-use form, and that there would be other, similar systems. It turned out to be 12 years before the TI-92 appeared and another few years before Casio came out with a competitor. And so the UCSMP curriculum from the start was influenced by the existence of what we now call CAS software, but even in its second edition it could not assume students would have access to CAS. Only in our last course, Precalculus and Discrete Mathematics, were there lessons using CAS.
In the meantime, my belief that technology helps in the learning of mathematics has not waned one iota. I believe that technology has to be a partner if we are serious as a society about reaching the goal of the slogan of 1989, “everybody counts,” or its current version, “no child left behind.” If we truly wish to improve the use of mathematics in society, we have a moral obligation to further the use of instruments that can give so much power to people. This talk is about computer algebra systems, but I hope that some of what I say will be applicable to the corresponding technologies for other branches.
Algebra in U.S. Schools
The population of students taking algebra in the United States has increased markedly in recent decades. A century ago, less than 15% of the age cohort entered high school and only they studied any algebra. By 1972, virtually all students entered high school and about 72% of them were taking one year of algebra. About half of these students took a second year. Algebra was still viewed as a high school subject and introduced before 9th grade to only about 10% of students. Yet by 1998, some algebra was being taught to virtually all students before high school, over 90% of students were taking one year of algebra by the end of the 9th grade, and 2/3 of students were studying a second year of algebra in 10th or 11th grade.
Perhaps because of this extraordinary increase in the percent of students taking algebra, most algebra courses show students applications of the subject. Because of technology, we now see graphing calculators in most second-year algebra and precalculus classes. But if you look at state standards and college placement tests, there has been very little change in expectations of what students should learn. We do not seem to expect students to learn algorithms that might be more appropriate given today’s technology. It is as if we showed 4th-graders all the paper-and-pencil ways of getting answers to multiplication problems and then didn't allow them paper and pencil to get the answers on a test.
People realize that they need to know arithmetic. Whole numbers, fractions, decimals, and percents are everywhere. Just pick up a newspaper or magazine, open to any page at random, and count the numbers on it. In almost every country, a daily newspaper has a median of about 125 numbers on its pages.
Society’s treatment of algebra is different. Scan a daily newspaper and you are not likely to see any algebraic formulas. Items for sale in stores have lots of numbers on them, but no algebra. Even scientific publications meant for the public and with lots of numbers in them tend to have little if any algebra. Adults may be handicapped by a lack of knowledge of arithmetic, but lack of knowledge of algebra does not seem too debilitating.
Because CAS makes it possible for students to do algebra virtually automatically, its use requires that we believe that all students should learn algebra. This rubs against a very common belief in society that algebra is not for everyone, either because (a) not everyone needs algebra, or (b) not everyone can understand the language of algebra (even if they can do it). To many people algebra is like Latin; it is the language of mathematical priests. Although certain words may come into our vocabulary, algebra is only a curiosity to most. As for calculus – it is like ancient Sumerian.
When people are required to learn a subject that they feel they do not need, will not use, and that requires work, there are predictable results. Many of them will dislike the subject and be proud of their dislike. Negative attitudes towards algebra are passed from generation to generation.
The Roles of CAS in Algebra
The difference between algebra and arithmetic in our society has major implications for the way we think about CAS. Most children get a lot of their intuition about numbers outside the classroom. The schedule of the day – when to get up, when to go to school, when to have dinner, when to watch a favorite TV program – involves numbers. Arithmetic is everywhere. Even in school, arithmetic is a social activity: children have to be at school at particular times shown by numbers, they go to a classroom with a number on it, they turn to a page in their textbook as told by their teacher, they do problems 1-20 for homework. Numbers are involved in many social interchanges.
Children learn how numbers are related to each other – what we sometimes call “number sense” – from these social interchanges more than from practicing paper-and-pencil skills or memorizing basic facts. We can see this because all children are taught skills and facts in school but they do not all learn number sense. But children in homes where people know mathematics do gain that number sense.
Algebra is different. There is virtually no algebra anywhere to be seen outside of school and technical discourse, so a teacher has the more difficult job of creating socialization in a class. This may be why some teachers emphasize writing and discussing the mathematics – the communication forces socialization. It seems to me that one way to get CAS into schools is to convince people that CAS changes algebra from being like Latin to being like their mother tongue, that it makes algebra comprehensible. We can say that we would like CAS to do for algebra what graphing calculators have done for functions. Graphing calculators have made it possible for all students to work with functions. We might argue that rational expressions and other complicated manipulations have been taken out of the curriculum in order to accommodate the increased number of students in our courses. CAS can help us get them back.
In this regard, CAS plays a particularly important role. CAS can exhibit patterns that a student will not see or encounter outside the classroom. This may be the most important reason for having CAS in schools. Students can learn how numbers are ordered by watching sports. They can learn about decimals by dealing with money. They can learn about fractions from recipes or measuring, and about percents from sales tax or political polls. They can learn these things without going to school.
But even the simplest algebra does not appear outside the classroom. 2a + 3a = 5a, the solving of x + 53 = 112, and anything involving variables is not found. When a student encounters xm • xn = xm+n, it is likely that that student has not encountered anything like that before – ever. No wonder students multiply exponents instead of add them, or multiply the bases. They have never seen the patterns. Better students see the patterns; or perhaps they are better students because they see the patterns. But many students need to see lots of correct examples before they notice that algebra works logically, not unpredictably. Thus, many teachers who have used CAS with first-year algebra students believe that these calculators are more valuable for their slower students than their better ones. This works against what is common practice in schools, namely, to give technology only to the best students. CAS is at least as valuable to the poorest algebra student as it is to the best.
Obviously we do not use CAS in the same way with slower students as we do with better students. For better students, and even for the average student, something can happen with CAS that I do not think has been fully recognized. CAS enables students to work with symbolic manipulation that we have avoided in the curriculum because of its difficulty. This is an important aspect of successful technology. It is significant that although there remains controversy towards the use of graphing calculators, there is quite a difference between the public's view of four-function calculators and their view of graphing calculators. Many in the public do not want simple calculators in elementary school because they feel that these calculators take away understanding. We know this isn’t necessarily the case, but it is a common view. On the other hand, there is a more tolerant view towards graphing calculators in high schools because the public never understood functions in the first place. They realize that graphs and lists and automatic calculation of function values do assist in an understanding that most people have never had without technology. In order to get CAS into the mathematics curriculum, we must emphasize the use of CAS to do things that cannot easily be done without it.
The ease with which CAS does what the public perceives as algebra gets in the way of one of the main reasons for learning algebra in the United States. Algebra is a gatekeeper. Without a knowledge of algebra, a person cannot go to a selective college. A person is kept from doing many jobs or even entering many job-training programs. Algebra is such a significant gatekeeper that Bob Moses has called the study of algebra a civil right. Recently, algebra – not just arithmetic – began appearing on high school graduation tests. For the first time, there are places where students cannot graduate without knowledge of algebra. Yet I know of none of these exit exams that allows the use of CAS. When CAS is universally used, algebra is no longer a gatekeeper. In order for CAS to be used, the idea of algebra as gatekeeper must be removed. The civil right is not merely the study of algebra, but the use of any available technology that might assist that study.
In the past, when only a very small percent of the population needed to learn algebra, we could be content with the algebra course as a gatekeeper. But today, when a good deal of algebra knowledge is expected from anybody who wants to continue in school after high school graduation or who plans to study any of a number of trades, we cannot afford to weed out so many students. Algebra needs to turn on students rather than turn them off. CAS in the curriculum must be exciting. It must help students understand why they are learning algebra.
Thus I believe that three attitudes about algebra need to be changed if we are going to have CAS for all students: the belief that algebra is not needed by all students; the belief that algebra is too hard to be learned by all students; and the belief that algebra should be used as a gatekeeper. To change those beliefs we need to stress that CAS makes some algebra, previously accessible to a few, accessible to all, and that CAS empowers students to do important mathematics that they could not do easily without it.
With all this in mind, let me now turn to the curriculum.
The Importance of Algebra
What is that important mathematics that CAS facilitates? And how is CAS related to it? For this, it is helpful to examine algebra in some detail and to ask why algebra is so important that its study is required of all educated people worldwide.
Algebra is the language of generalization. As a result, it enables a person to answer all the questions of a particular type at one time. Algebra is also the language of relationships among quantities. This makes algebra a powerful language for solving certain types of problems. Algebra is also the study of structures with certain properties.
Through its descriptions of generalizations and structures, algebra – more than any other branch of knowledge created by humans – shows that our universe possesses order. And because it has all these properties, algebra is the basis for virtually all mathematics and is a fundamental tool for dealing with the generalizations, relationships, problems, and structures in many other disciplines. This is why algebra is important.
Unfortunately, instead of being taught as a living language with a logical structure and many connections between its topics and other subjects, algebra is often taught as a dead language with rules that seem to come from nowhere. That so many well-educated adults wonder why they studied algebra is testimony to the disjuncture between this important subject and the way it is presented in schools. If CAS is used in a traditional algebra classroom, taught without applications and with algebraic manipulations taught only for their own sake, it will not be much of an advance.
If algebra is so important, how is it that people live without it? They do, but they cannot appreciate as much of what is going on around them. They are like us when we travel to another country and do not speak its language. We understand very little of what we hear, and we do not understand or appreciate as much of what we see as the natives do. CAS serves as both traveler’s dictionary and guidebook.
Today’s pasteurized and homogenized algebra
The algebra that we teach in grades K-12 is purposely pasteurized and homogenized. It is pasteurized when it is stripped of difficult coefficients and cleansed of non-integer solutions. It is homogenized when the problems are of certain predictable forms. In a section on the solution of quadratic equations, we know that there will be certain kinds of problems: some in the form ax2 + bx + c = 0; some in the form a(x – h)2 + k = 0, and perhaps some easy variants of these forms. There are rarely equations of the form
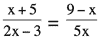
or equations involving irrational coefficients or complex coefficients. The variable x will appear more often than any other. And there are almost never equations for which a standard algorithm does not exist.
By mentioning the pasteurization and homogenization of algebra, I do not mean to deride these ideas. There are good reasons to use canonical forms, to keep things simple. We want students to have things in mind when they read certain words or see certain symbols. But this cleansing and simplification of algebra means that, for the standard algebra that is taught to most students, there is not very much need for the power of CAS. It is as if we are teaching arithmetic using numbers with no more than 3 digits and we come in with a calculator that manipulates 12-digit numbers. The need for the power is not particularly clear.
Thus, in order to get CAS into the K-12 algebra curriculum, expectations have to change. Not just conceptual expectations, such as an earlier emphasis on functions, but also procedural expectations, namely, the algorithms students are expected to master.
The last of my general observations is that we need to take into account the fact that technology itself needs to be learned. A child needs to begin with simple technology in the early grades and then gradually be introduced to more sophisticated technology in later grades.
Opportunities for CAS
Here are just a few of many possible examples of what CAS might do at various grade levels K-12.
Grades K-3
Every child needs to have a piece of hardware – such as a calculator or computer – that has numbers and letters on it and can graph. The technology needs a screen that one can write on just as one writes on a slate when signing for a charge at some stores these days. It should record paper-and-pencil work as well as computer work, so that any work the child does can be brought up as a record.
Whatever is done at grades K-3 has to be a part of literacy. Fortunately, there is widespread software that can be viewed as rudimentary CAS: the spreadsheet. Most spreadsheet users do not think they are doing algebra when they use Excel and other spreadsheets because this does not look like school algebra, and because algebra is supposed to be hard. Because spreadsheets do not look like algebra, elementary school teachers do not have the fear of them that they would have of technology that more obviously incorporates algebra.
We should take advantage of the fact that working with a spreadsheet is algebra. The names of the variables are A1, A2, A3, ..., B1, B2, .... Each time we ask the spreadsheet to calculate something and put it in another cell we are writing an algebraic formula. For example, if in cell C1 we type “= A1 + B1,” then we are naming the variable C1. The spreadsheet does the calculation for us, of course. Each time that we copy a formula to other cells, we are creating a function. The function may be explicitly defined or it may be an iterative sequence, but it is a function either way. Most spreadsheet programs allow us to graph the explicitly defined functions. With the graph or successive approximation, we can solve many equations. Also, almost all spreadsheet programs have a form of summation notation that makes for a very easy transition to traditional ∑-notation. Sum(A1:A5) is so similar to 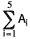 .
.
Thus algebra capability is in most every computer, on virtually every business desk. And people who think they know no algebra are using this capability.
There are many things spreadsheets can do. Charts can automatically change as entries are changed, showing variability and patterns. The introduction of a spreadsheet is a very nice way to introduce CAS quite early. Not only that, but the large commercial publishers already have rudimentary spreadsheets as a tool in the K-6 programs available on line. This could spur them to upgrade that technology.
Grades 4-6
In grades 4-6, we can obviously do more. Here is a use of a variable as an argument in an algorithm. Think of an integer. Add 2. Now multiply it by 3. Now add 4. Now multiply your number by 2. Now subtract 8. If you divide by 6 and tell me what you got, I can tell your original number. It is 2 less than the number you just provided. Here the first number is a variable acting not as an unknown but as an input number in an algorithm. By putting the variable in a spreadsheet, it has become a placeholder. Then the variable becomes an unknown because I am playing a game. The spreadsheet here shows the workings of the game for numbers chosen from 1 to 35. The screenshots below show how CAS can be used to explain why the number trick works.



The use of variables as inputs is perhaps the easiest use of variables for students to learn. Almost all students find it very easy to evaluate algebraic expressions. It is something for us to take advantage of.
A more conceptual use of placeholders has to do with place value. The notion that a two-digit number with tens digit t and units digit u has value 10t + u is difficult for many students. But with a spreadsheet it is easy. Not only that, but we can go much farther. We can go to decimals and speak of 100A1 + 10B1 + C1 + .1D1 + .01E1 and so on. By changing values in columns A-E, we see how the value of the number in column F changes.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1> | 2 | 3 | 8 | 0 | 6 | 238.06 |
Grades 7-9
You can ask a CAS to solve an equation such as ax + b = c. With paper and pencil, you expect the solution
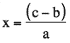 .
.
But with a CAS, you are often forced to consider equivalent expressions. One CAS shows
 .
.
Thus an activity that is often meaningless, showing that -( b – c) = c – b, is needed. A CAS can show the equality.


You can also ask to solve for b and find b = c – ax.
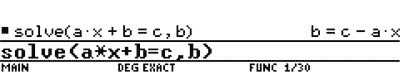
This is what CAS is known for, symbolic solutions to equations.
CAS also has many instructional uses. Consider the following equation.
6x – 40 = 12 – 8x
Currently available CAS enables students to explore what happens when they do various things to both sides. Add 6x to both sides, or 40, or -40, or 12, or -12, or 50x, or -8x. In a non-threatening environment, students quickly see that some additions lead to simpler equations and others do not.
Add 6x to both sides.
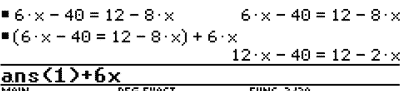
Add 40 to both sides.
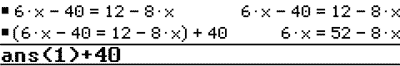
The entire solving process can be emulated on a CAS.
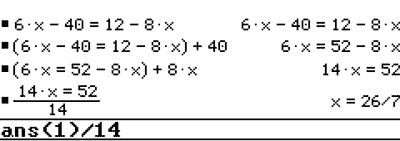
Some CAS technology today enables algebraic spreadsheets. Consider this pattern.

Now we see that x2 – a factors over the integers when a is a perfect square.
Here is another pattern, a little more complicated.

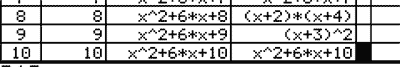
It is important to use CAS to get insights into and beyond the mathematics we teach, and not just use CAS because it can do manipulation more quickly and accurately. We must do things we could not do before. There is no sense using CAS for the algebraic equivalent of multiplying 11 by 13. It certainly is possible that judicious use of CAS might improve paper-and-pencil skill. The goal of mathematics is not, to me, the ability to do things with paper and pencil. The goals of mathematics learning are competence with problems, understanding of the mathematics, communication of that mathematics to others, and the ability to use deduction to demonstrate the validity of mathematical results. Skill, obtained by any technology, paper-and-pencil or electronic, is only a means to those ends.
Grades 10-12
At a CAS conference last year, Carolyn Kieran spoke about the factorization of xn – 1 into (x-1) and (xn-1 + xn-2 + … + x + 1). But why is this important? I would note that this might be used to obtain the sum of a finite geometric series as found in problems involving annuities such as mortgage payments. Good situations are those that are not approachable or difficult to approach without CAS, or those for which CAS lends insights not easily attainable otherwise. For instance, a problem related to Kiernan’s example is Cebotarev’s problem.
Consider the prime (or irreducible) factorization of xn – 1, for integers n > 1, over the integers. For example:
x2 – 1 = (x – 1)(x + 1)
x3 – 1 = (x – 1)(x2 + x + 1)
x4 – 1 = (x – 1)(x + 1)(x2 + 1)
Prove or disprove: For all n, the coefficients of the prime factors of xn – 1 are either 0, 1 or -1 (N.B. Cebotarev, 1938).
The answer is surprising. There is rich mathematics here and also a rich application.
Once students have had some algebra and geometry, the opportunities for CAS greatly increase. The dynamic algebra is naturally applied in dynamic geometry software such as Cabri and Geometer’s Sketchpad. With good students, we might use CAS to show the analytic geometry that is behind geometry drawing programs. It seems a fruitful area for exploration.
Another area that is rich in history and used to be important in the education of future mathematicians is the area of polynomial solutions. In the UCSMP course Precalculus and Discrete Mathematics, we show an example of how the real and non-real roots of a 4th degree polynomial equation move in the complex plane as the constant term increases. There is rich mathematics here, not just in the graphical representation of the roots, but also in the relationships between the roots and the coefficients of the polynomial and in various methods used to approximate these roots. Fifty years ago, a standard college mathematics course entitled “Theory of Equations” was devoted to this kind of mathematics. The manipulation required for this mathematics is formidable but now can easily be done.
The Case for CAS
A very nice book outlining a strong case was written last year under the auspices of T3 Europe. Three arguments are given for CAS:
- The teaching of mathematics becomes more interesting with CAS.
- Students are more motivated to learn with CAS.
- Students who use CAS are at least as good in “pencil and paper” skills as their traditional counterparts.
- CAS brings home the need to be able to recognize and operate with equivalent expressions.
- CAS enables students to see algebraic patterns that would be practically infeasible to obtain without it. This makes CAS particularly important for students having trouble in algebra.
- Whereas graphing calculators enable students to see how the change in a parameter affects the graph of a function, CAS enables students to see the symbolic power of parameters. This makes CAS particularly useful in extending solutions to problems to obtain generalizations.
The authors go on to assert that high stakes assessments and CAS are compatible. In this talk I have given three more reasons for students to have and use CAS while they are learning school mathematics.
The Coda
Paper-and-pen and, more recently, paper-and-pencil has been the technology that we have used for the past 400 years to do arithmetic. Paper-and-pen became dominant not because people understood why the algorithms work. They still don’t! Paper-and-pencil won because its algorithms were more widely applicable. I believe we are now in the same situation with computers and algebra. Ultimately - not in my lifetime but perhaps in some of yours - the computer algorithms embodied in spreadsheets and automatic graphers and CAS systems will become the algebra that everyone uses and recognizes. Spreadsheets will be employed to help introduce the language of algebra to students, and CAS systems will be used to perform the complex manipulations.
This does not mean that paper-and-pencil algebra will become obsolete. It will not become obsolete any more than mental arithmetic has become obsolete. People will still need to know how to solve simple equations and do simple manipulations by hand. And, perhaps more important, they will need to be able to translate from real and fanciful situations to mathematics and vice-versa. Algebra is more important than ever. CAS does not make school algebra obsolete, but school algebra needs to change to touch the everyday lives of students and their families in order to be relevant to all students, and in order for the public to be comfortable with technology that makes algebra accessible to all.
Many, if not most, mathematics teachers in the world do not have much experience with this algebra. Even some talented mathematicians and many of the best mathematics teachers in the United States do not view algebra in this light. So, in our task to have our students learn the best mathematics we can deliver, we have a number of jobs to do: to work out the best mathematics curriculum we can using widely available technology; to encourage the development of inexpensive technology and materials for teachers and students for that curriculum; to help our colleagues and future teachers become able to deal with these ideas; and to get messages to the public that will make them support the use of such a curriculum. We should be able to say: Now that CAS exists we, with our students, can devote more time to the underpinnings, to the applications, and to the representations that provide a deeper understanding of mathematics. What happens to mathematics now that there is CAS? It gets better!
At UCSMP, we are committed to making use of CAS technology in the third edition of our secondary curriculum because we are committed to giving our students the best possible mathematics and the best available tools for learning that mathematics. We understand that ETS is also working on a curriculum that will use CAS heavily. The NCTM Central Regional Conference in Chicago in September 2006 had a large and meaty CAS strand.
The importance of mathematics has put a lot of pressure on those of us in mathematics education to make it possible for all students to gain a higher amount of facility and understanding in mathematics than ever was expected before. Not to use CAS to help in this venture is to deny ourselves and our students an extraordinarily useful tool to gain that facility and understanding. To deny students the use of such tools is as unwise as denying them paper and pencil. We have a moral responsibility to make this power available to all our students.
Contact
UCSMP
1427 East 60th Street
Chicago, IL 60637
T: 773-702-1130
F: 773-834-4665
ucsmp@uchicago.edu