• Papers from Conferences
• Applying Arithmetic
• Translations
• Van Hiele Levels & Achievement

Algebra and Calculus for All?

Presented November 11 and 12, 1995

UCSMP Director Zalman Usiskin presented this talk at the Eleventh Annual UCSMP Secondary Conference, held November 11 and 12, 1995. This article was published in UCSMP Newsletter No. 18: Winter 1996.

The motivation for this talk comes from three different sources. The first is a longstanding belief of mine that not only do algebra and calculus play analogous roles in high school and college, but almost all the issues that apply to one also apply to the other.

The second source for what I am about to say came in June 1994, when I was asked to give a talk at a calculus conference in Ann Arbor, Michigan, sponsored by the Calculus Consortium based at Harvard University. The rhetoric used to discuss calculus reform at that conference was virtually identical to the rhetoric we have been using at UCSMP. This year we decided to invite the five NSF-supported calculus projects to present at this meeting. All five accepted our invitation, and we are very happy to have them here. This is the first time that we have ever invited other projects to our meetings, and we will be interested in your response to this idea.

The third spur for this talk came in January 1995 when Texas Instruments announced that by the end of the year they would be selling a calculator that could do algebraic, dare I say abstract, manipulation. This calculator performs not only the manipulations one normally finds in algebra but also those found in calculus. But it is not the first technology to make us wonder about the relationships between algebra and calculus. Since the first function-graphing program, there have been obvious questions about how much manipulation is necessary to graph a function or to find its maxima or minima on an interval, two tasks that have been among the major reasons for studying calculus. Since the TI-92 calculator has indeed debuted right on schedule this week, a talk discussing issues related to it seemed appropriate.

The Parallel Roles of Algebra and Calculus Courses

The terms “algebra” and “calculus” each describe a realm of mathematical thought: calculus is the area of mathematics known to mathematicians as analysis, and algebra is part of the field of mathematics that studies algebraic structures. But these two terms are also strongly associated with two specific courses. Algebra and calculus courses play parallel roles in high school and college in many ways.

Algebra and calculus are each fixtures of the curriculum, the first course, a sign of arrival. Algebra is the first course in high school mathematics. If you take algebra before ninth grade, you are said to be taking it early. If you do not take algebra in ninth grade, you are taking remedial mathematics. Calculus is the first course in college mathematics. If you take calculus before your freshman year of college, you are taking it early. If you do not take calculus your freshman year, you are taking remedial mathematics. Thus algebra and calculus are fixed in time and place as the first year, usually in a new school. They are each signs of having arrived at a new level of schooling.

Algebra and calculus are prerequisites to a great deal of future work. Algebra is the necessary precursor to the rest of high school mathematics. Whether or not you use much algebra in your geometry course, you must pass algebra to get into geometry. Calculus plays the same role for college mathematics. You may not use much calculus in your abstract algebra course, but you won’t be allowed in unless you have passed calculus.

Algebra and calculus are normally offered at various levels of difficulty. Not everyone goes on to take more mathematics beyond these courses, so there have developed various levels: Honors level. Regular level. Basic level. Courses taught with rigor for the better students. Courses taught as drill and practice for the lower-performing students.

Algebra and calculus courses are filters. If you are a student in the lowest of the levels, you are greatly handicapped if you wish to go on to take more mathematics. You do not have the prerequisites. If you do not perform well at the level you take, whether it be a high level course or a low level course, you will be dropped a level.

But algebra courses and calculus courses are different filters. No one wants algebra in high school to be a filter. On the other hand, college calculus is required for some majors in order to discourage people from taking that major. In many places, business majors must take calculus although many never encounter its uses while they are undergraduates. Calculus is an overt filter; algebra is more covert.

Algebra and calculus are each taken a year early by the best students. In 1955, the Advanced Placement program of the College Board began, and calculus began to be offered to the best twelfth grade students. At the very beginning, most schools tried to cram four years of high school mathematics into three so that they would have students ready for the AP exam, but after a while it became more popular to offer an eighth grade algebra course. Now an eighth grade algebra course for the best students is a fixture in most school systems.

Algebra and calculus courses each tend to be designed to be harder when taken earlier, because the accelerated students are taking them. The AP calculus course is not easy. In many schools, the eighth grade algebra course is harder than the corresponding ninth grade course. There is a justifiable reason for this: the best students can handle such a course. But that means that many more students could take the course earlier if it were not made so difficult. At UCSMP we think that average eighth graders can and should take algebra, and the best can do it at seventh grade. Although algebra in the eighth grade is being taken by an increasing number of students—estimates range now from 20 to 30 percent of eighth graders—it is still not standard practice. Yet in some countries, seventh graders normally study some algebra and eleventh graders begin calculus.

Some people think that algebra and calculus concepts can be learned much earlier and that the usual grade levels are far too late. Henry Borenson touts his Hands-On Equations for third, fourth, and fifth grades, the same students to whom Project SEED has been teaching algebra ideas for a couple of decades. And many years ago I received Calculus for Seven-Year-Olds written by Don Cohen of Champaign, Illinois. Thus, although the courses have fixed places in the traditional curriculum, there are many who believe that the ideas could be taught much earlier.

With both algebra and calculus, hurdles are in place to discourage early work with the subject. When the student comes to a high school having had an algebra course, the student is examined closely. He or she is very likely to be given a difficult test, increasing the likelihood that the score will not be high enough to pass out of the algebra course. The school does not trust others to teach algebra. The school does not want to consider the fact that when you take a course from one teacher and then have to take a final exam months later written by someone else, you are unlikely to score as high as if you had taken the course from the exam-writer.

Similarly, colleges do not trust high schools to teach calculus. A college placement test does not necessarily cover the course content students have had, but the results are used to justify not allowing a student to place out of a semester or two of calculus and often to put a student back a year or two.

All of these similarities between algebra and calculus have almost nothing to do with the actual content of the courses. So now let’s look at the mathematics itself.

Parallel Views of the Content of Algebra and Calculus

All our lives we have been taught (as our parents and grandparents were taught) two statements as axioms about mathematics. First, that mathematics is abstract. Taken consecutively (we have been taught) the concepts in each mathematics course are more abstract than the last. Algebra? More abstract than arithmetic. Calculus? More abstract than algebra. This view of mathematics gives unsuccessful students an out. We can say that they learn concretely, they are visual learners, they need practical examples, and abstract mathematics just doesn’t fit the bill.

Having decided that mathematics is abstract, the second supposed axiom presents itself: that mathematics is difficult. Again here we are taught to believe that mathematics has increasing levels of difficulty. Algebra? More difficult than arithmetic. Calculus? More difficult than algebra.

These views are deeply ingrained in the psyche of many mathematicians and mathematics educators. As a result, often it is considered bad mathematics when math is not taught abstractly or when students proceed through courses without difficulty.

Those who are unsuccessful in mathematics can take refuge in their ignorance, because, it is said, “not everyone can learn mathematics.” Those who are successful in mathematics can bask in the glory of having succeeded where only a minority achieve success and wallow in the pride of knowing what only a few are granted the opportunity to acquire.

Thus, as a consequence of these two mistaken beliefs, society concludes that algebra is not for all students and calculus is for even fewer. Because algebra is more abstract than arithmetic, many elementary school teachers avoid algebra entirely, and many high school teachers want it that way. They would prefer that a student come in without having had any algebra so that they can teach the student from the beginning. And so it is with calculus. The concept of infinite processes leading to limits is viewed by many calculus teachers as a very difficult idea. Calculus teachers are notorious for wanting high schools not to teach any calculus, not even introductions. And some high school teachers go along with this and do not introduce calculus ideas for fear of doing something wrong. A very common belief thus arises, that early work in these areas is unwise except for the small percentage of very bright students.

An Alternative View of Algebra and Calculus

In 1623, Galileo wrote in The Assayer:

Philosophy is written in this grand book, the universe, which stands continually open to our gaze. But the book cannot be understood unless one first learns to comprehend the language and read the letters in which it is composed. It is written in the language of mathematics, and its characters are triangles, circles, and other geometrical figures without which it is humanly impossible to understand a single word of it; without these, one wanders about in a dark labyrinth.

At the time of this writing, algebra was in its infancy, and analytic geometry had yet to be invented. There was no probability theory. The basic vocabulary and symbols of calculus would be introduced about sixty years later by Newton and Leibnitz. The f(x) function notation, the symbol for p, and the abbreviations sin and cos would not come into the language until Euler, over 100 years later. The invention of statistical displays—bar graphs, circle graphs, and the like—was even further in the future, and statistical theory was nonexistent.

The language Galileo wrote about was only a small piece of the edifice that we call mathematics. The language available to Galileo described only part of the physical world. Today’s mathematical language underlies financial dealings worldwide; describes a wealth of characteristics of all sorts of phenomena; is integral in high-speed communication through words and pictures; and models far more of the physical world than in Galileo’s time.

All of our work with UCSMP and before has convinced me that mathematics is not inherently the most abstract of subjects, but is made so; that it is no more abstract than English or any other language. It has also convinced me that mathematics is not inherently the most difficult of subjects, but is made so. It is no more difficult than learning a new language. Furthermore, just as it is more difficult to learn a language when you are older, the very delays that we think make it more likely that children will succeed in learning algebra and later calculus make the subjects more difficult.

What Have We Learned about Algebra?

In exploring alternatives to the received wisdom about mathematics, what have we learned? Let’s look at algebra.

Students’ use of algebra starts earlier than formal algebra study, whether we want it to or not. The equation 3 + [ ] = 7 is algebra. The use of an empty square box is no different than the use of a letter. So first or second graders do algebra problems, but we just don’t tell them. Perhaps we don’t want to scare the teachers. For many decades, formulas like I = prt and A = πr² have been studied prior to algebra. Additionally, now almost everyone introduces students to graphing, to equation-solving, to properties like the distributive property, before the formal course called algebra.

We have learned that the use of applications concretizes algebra, provides a motivation for it, and makes it easier. We can approach algebra theoretically, such as through field properties, but this approach does not work with many students. We can approach algebra through formulas or generalizations of patterns, and this approach does work although it isn’t automatic. It doesn’t come in one day. But situating the algebra in contexts which give reasons for studying the subject at the same time that they illustrate the concepts changes one’s view of algebra forever. I know there are many here who could not return to the way they used to teach algebra.

We have also discovered that there is no age cut-off with respect to learning the concept of variables. We should not have been surprised at this. Variables are supposed to be an abstract concept, but they are introduced quite early in some countries’ curricula, such as the Soviet Union, and seem to be easier to learn early. Is the use of the letter A for area or x for an unknown any more abstract than the use of the symbol p for the sound “puh”? Surely, there is an age cut-off. Babies will not learn variables. But at the secondary level, from grade 6 or grade 7 up, it seems that the earlier the better.

I do not wish to be interpreted as believing that you can just go in and learn algebra. We have seen that there are in fact prerequisites to learning algebra. If a symbol is to stand for a number, as variables usually do, you have to know something about numbers. You have to know that a number can be represented in many ways, that 6 can be written as √36 and as (12/2) and as 6.000, and that if x = 6, then x can be written in any of those ways, too. You need to know what it means for one number to be close to another in value. If you have the expression x + y, you need to know what the plus sign means independently of what the numbers x and y are. In UCSMP, we work on these meanings before the concentrated study of algebra because such work is necessary for success in algebra.

We have learned that the distinction between arithmetic and algebra is often hard to make. Suppose you are working with a spreadsheet. You instruct the computer to take the numbers in cells A2 and B2 and put the sum in cell C2. So you write =A2+B2 in the cell C2. Are you doing arithmetic or algebra? Technology has blurred the distinction between the two. While working with spreadsheets and graphics technology, students use algebra without realizing it.

The distinction was blurred, however, well before there were computers. Consider any triangle ABC. Is A a variable? It is in the sense that it may stand for any point. But we think of it as a specific point because it is such a familiar idea.

When I studied algebra, plotting points on the coordinate plane was considered algebra. So was any work with negative numbers. My classmates and I never did one day of that work before algebra. Since then, we have seen that graphing and negative numbers are easy when they are contextualized, and so we are comfortable today not calling those concepts algebra. Thus, virtually all middle school or junior high school students are learning algebra today, whether or not they take a formal course with that name.

All that we have seen about algebra leads us to conclude that virtually all students can learn algebra!

Does What We Know about Algebra Apply to Calculus?

Does all this apply equally apply to calculus? In other words, are these statements true?

• Calculus starts earlier than its formal study, whether we want it to or not.
• The use of applications concretizes calculus, provides a motivation for it, and makes it easier.
• There is no age cut-off with respect to the learning of limits.
• There are prerequisites to learning calculus.
• The distinction between algebra and calculus is often hard to make.
• Virtually all students can learn calculus.

Let us take each of these one at a time.

Calculus starts earlier than its formal study, whether we want it to or not. Students are first introduced to limits well before their first calculus course. Infinite decimals involve limits. In geometry, students see limits of inscribed and circumscribed polygons for approximating π. In the case of volumes, there is Cavalieri’s principle which suggests the idea of finding volume by summing very thin slices. The volume of a sphere is the sum of the volumes of infinitely many pyramids. There are the successive approximations of solutions to equations, and of course there is rate of change. So the ideas of calculus start earlier than its formal study, whether or not we want that to be the case.

The use of applications concretizes calculus, provides a motivation for it, and makes it easier. Most of the calculus materials that are represented at this conference make strong use of applications for the very same reasons that we use applications in all the UCSMP secondary courses. The authors of these materials know that calculus can be approached theoretically (through ε–δ definitions, for example) but such an approach does not work with many students.

There are prerequisites to learning calculus. Students must be familiar with slope and rate of change from algebra; with area and volume formulas from geometry; with summation notation; with function notation. They must be able to chunk algebraic expressions so that they think of f(x+h) – f(x) as a single number, and not as some indecipherable expression. And very importantly, they must learn to think of a function as a single object that can be represented in various ways, for instance, by a graph, by an equation, by a rule. They must be able to distinguish the function f from its values f(x).

The distinction between algebra and calculus is often hard to make, thanks in part to technology. Suppose you are asked to determine the maximum point of the function V, where V(x) = x(20 – 2x)(24 – 2x). This function V may look familiar, and it can be found in UCSMP Advanced Algebra. It is the volume of the rectangular surface formed by cutting out a square of size x from a 20 by 24 rectangle, and then folding up the sides. If you use the trace function on an automatic grapher to estimate this maximum, are you doing arithmetic, algebra or calculus? An algebraic expression is being evaluated, but the grapher is doing the calculation automatically and all you see are the arithmetic values. Yet you are working on a calculus problem.

All algebra teachers in all algebra courses have students who solve algebra problems without doing formal algebra. They use arithmetic. So it should not surprise you that calculus problems can be solved without formal calculus.

In the algebra of even a decade ago, we might have multiplied the three factors of V(x) to represent V(x) as a polynomial so that we could differentiate V with respect to x more easily. But if we can find the answers to max-min problems without formal differentiation, we don’t need that manipulation. Even before the existence of a symbol manipulator, the technology took away our motivation to do some of the manipulation in algebra.

But computers are not required to blur the distinction between calculus and other areas of mathematics. When calculus ideas are used in geometry, or infinite sums are shown for an infinite decimal, the ideas of calculus lurk but few students realize it. And we have found no age cutoff with respect to that learning.

Can all students learn calculus? It is hard to believe they can’t, if the approach is reasonable. Should all students take the course called calculus? That is a different question, one beyond the scope of this talk.

Algebra and Calculus K-12 and the Question of Integrated Curricula

Today, some people cringe when they hear talk about an algebra course. Mathematics knows no strict boundaries, they say. There should not be a full year devoted to algebra. People have said this about calculus, too.

As many of you know, I have either authored, co-authored, or actively edited virtually every page of the UCSMP texts and teacher editions for secondary school students. Before UCSMP began, I had authored or co-authored four texts for each year of high school. All these courses tended to integrate areas of mathematics that had often been separated: transformations and matrices in Algebra and Geometry; applications into all courses; algebra and geometry considered in the first four UCSMP courses; functions and statistics combined in Functions, Statistics and Trigonometry; the discrete and the continuous interwoven in Precalculus and Discrete Mathematics.

Yet I have been uneasy with those who believe that our curriculum should be decompartmentalized. One reason I have been uneasy is that I believe the UCSMP courses are more integrated than many of the curricula that other people call integrated, including the curricula of Japan or the Soviet Union or the curricula written to follow the New York State Regents exams. To me, an integrated curriculum must have connections not only within lessons and chapters and units, but also between and among the units. One of the major developments in mathematics early in this century was the demonstration that all mathematics, from arithmetic to geometry, from sets to calculus, could be considered as part of one logical system. Consequently, covering a collection unrelated mathematics topics in a given year without relating them is not integration, but disintegration. It destroys one of the most basic principles underlying the field of mathematics.

Still, there is an important reason for not having the traditional one-year algebra course. In the past, only the best students really understood the traditional year course in algebra when they were finished. Almost no country in the world tried to do what we tried with first year algebra, that is, to familiarize students who had almost no experience with the subject with some of the most complicated aspects of manipulation of the symbols, all in one year. This practice results in failure for a significant number of students.

But we have learned how to avoid most of the failures. Introduce students to the main ideas of algebra well before making them central in a course. Develop algebraic ideas in context, not as symbols without meaning. While concentrating on algebra, involve all other mathematics both as motivation for doing the algebra and as avenues for application. Finally, do not expect the most difficult ideas to be learned in one year, but return to them again and again as often as needed. Yet in many schools, these principles are still not followed. If you have that traditional view of how algebra is taught, you are correct to want to change it.

At UCSMP we have followed all of these principles. In the UCSMP curriculum, we have also applied these principles to calculus. The main ideas of calculus are introduced over six years, as the chart here shows (page 12). The abbreviations indicate the six years of USCMP secondary school texts: TM Transition Mathematics, A Algebra, G Geometry, AA Advanced Algebra, FST Functions, Statistics and Trigonometry, and PDM Precalculus and Discrete Mathematics.

Idea	Where Treated
Inequality	all six courses
Distance with coordinates	all six courses
Area	TM, A, G
Rate	TM, A, G, AA
Infinity	TM, G, AA, FST, PDM
Rate of change	A, AA, FST, PDM
Sequence	A, AA, FST, PDM
Function	A, G, AA, FST, PDM
Limit	G, FST, PDM
Areas on coordinate systems	G, AA, PDM
Max-min	G, AA, FST, PDM
Summation notation	AA, FST, PDM
Derivatives	PDM
Integrals	PDM

Virtually all of these ideas are developed in context and (except for derivatives and integrals) more than once before the student studies a formal calculus course. We think this is an optimal way to prepare students for calculus.

In general, one might say that the normal approach is the best approach for studying an area of mathematics. This means make an area the center of attention for some period of study, but look at that area before and after that period, too.

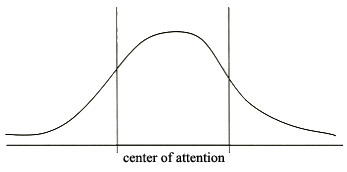
There is a moral to this for calculus. The current year- or year-and-a-half-long calculus course is unwise if students have seen none of the material before. But if attention is given to the major concepts in many of the preceding years, then it is a good idea to put all those ideas together, synthesize them, show how they are all related

Algebra is so important that we concentrate on it twice, in UCSMP Algebra with major thought to variables in expressions, in Advanced Algebra with more attention to expressions in functions. A bimodal normal curve represents this approach. We don’t give up algebra in between the two modes or before or after the two years in which there is concentration. I think that some of the newest integrated curricula agree with this idea, but want many more modes–perhaps one mode for algebra each year. Maybe calculus should be done that way, too. The jury is still out.

Regardless of your view about integrated curricula, the best approach is to develop an area over many years. Then, when the time is ready, the area should be studied in some detail. That way all of the ideas that were done separately over the years can be seen as related to each other. Logical connections can be made. Students can see what is known and what is not known about the area, what problems are simple and what problems are quite difficult.

While this is being done, other areas should not be neglected. Calculus and geometry and probability and statistics are passengers on the algebra train, but when the calculus train comes, it needs its own passengers–some algebra, geometry, probability, and statistics from earlier years, but also differential equations, complex variables, algebraic structures that students might encounter in later years. College students' lack of exposure to the latter topics in early undergraduate mathematics courses is surely one of the reasons they have difficulty with them in later undergraduate mathematics.

As an aside, all of this applies to geometry. To introduce geometry with a full year course is silly. It takes a while to learn concepts like measurement, similarity, congruence, and transformations. That is why the UCSMP curriculum pays strong attention to geometry both before and after the one year in which geometry is the centerpiece. That attention is absolutely necessary if you wish students to perform well.

The Question of Manipulative Skill

So far, this analysis of algebra and calculus has dealt primarily with the P, U, and R of the UCSMP's SPUR approach to learning, that is, with the properties, uses, and representation dimensions of understanding mathematics, what some people have called the conceptual understandings of mathematics. Now let us turn to the question of S, manipulative skills.

From the beginning of UCSMP, we have been influenced by the availability of symbol manipulators, that technology where you can input ax = b without specific values for a and b, and get x = b/a as output; input two rational expressions to be added, subtracted, multiplied, or divided, and get the sum, difference, product, or quotient in lowest terms; input a polynomial of virtually any degree and get its factored form either over the rationals, reals, or complex numbers; input an equation for a function and get its derivative; input a definite integral and obtain its value; or input an indefinite integral and obtain an expression for it.

Symbol manipulators were available on large mainframes even twenty years ago; they became available on smaller machines in the early 1980s before UCSMP began; they became available in user unfriendly form on calculators at least a half-dozen years ago. This week they became available in user friendly form.

Many of the skills in algebra are important regardless of the later mathematics one wishes to study. Squares and square roots are found in geometry and statistics and physics. Linear and exponential equations and functions are found here, there, and everywhere, as the song goes. Applications can be found for polynomials, too, and we have them in our books. And there are applications of rational expressions and rational functions, but not as many of these, and they are not so elementary, so we delay them until Precalculus and Discrete Mathematics.

But much of the manipulation in traditional algebra courses is contrived so that the student can do the further contrived manipulations that will be encountered in calculus. As an example, consider this question from a traditional algebra course:

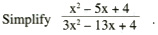
It is not found in UCSMP Algebra or UCSMP Advanced Algebra. Why was it in traditional courses? Mostly because years later students might encounter the following question in a calculus course:

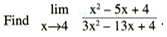
Now, at the time of calculus we might argue that a student ought to be able to factor a quadratic by hand, but for UCSMP students that is three years after Advanced Algebra. Consequently, we could not justify this kind of manipulation until our precalculus and discrete mathematics course. When studying rational functions, there is more than a contrived reason for such manipulation.

But it’s not clear to me that students of the future even need to be able to do this kind of manipulation by hand. The purpose of the calculus exercise is not to factor the numerator and denominator; it is to notice that there are ways to analyze limits even when both numerator and denominator of a fraction are zero at the limit. Once we know that, we can ask technology to do the factoring. The advantage of asking technology to do the factoring is that we concentrate on the idea rather than on the technique, on the end rather than the means. Without the technology, we may feel limited in the types of expressions that can be dealt with by this technique. The technology shows us the power of the technique.

One of the interesting things that technology does is make us aware of techniques that we may have not have ever been taught, of if taught, we may not have mastered. We can obtain partial fractions with ease whenever we wish and now ask the important question: why do we want partial fractions? Many students learn to separate out a rational expression into partial fractions, but have no idea why they are doing that. It is no different than a student who struggles with long division and then, after mastering the algorithm, is not able to recognize the situations in which division is needed. No student should leave an algebra course without being able to recognize situations in which algebra is appropriate. An adult of the future might ask, “Why did I take algebra?” But no adult should ever ask what algebra is good for.

Inexpensive technology that does algebra—and we expect that the technology will become cheaper—will enable us to concentrate even more on the whys of mathematics. We will be able to teach students why algebra is important and why calculus is important without being burdened by the need to teach them how to deal with every expression or function. And we will no longer have to say that you have to learn this or that paper-and-pencil skill because it is needed for calculus.

We must not forget that the general population today views complicated algebra and even easy calculus as the province of an elite few. Will you tell your friends that you spent your weekend at a conference to learn about teaching algebra, geometry, statistics, and calculus? You know what many of your friends think. Either they see you as a genius or as weird. Take heart that this is the way that people who knew arithmetic were viewed five hundred years ago. Technology algorithms make algebra and calculus automatic just as our long multiplication and long division algorithms have made arithmetic automatic. In the long run, they will make algebra and calculus available to all and much less threatening.

What Are the Messages for Today?

So what are the messages for the algebra student and teacher of today? The first is that algebra is a language with a set of skills, properties, uses, and representations that is not learned in a single year or two. Like other languages, it takes many years to become fluent in it, and even students who have studied it for four or five years may not achieve that fluency. Learning the language should start in elementary school. In USCMP Transition Mathematics you are still at the early stages. In Algebra you first visit the country in which this language is native. In Geometry you apply that language widely. In Advanced Algebra you revisit the country, and then in Functions, Statistics and Trigonometry and Precalculus and Discrete Mathematics and throughout your study of mathematics and its applications you use this language, continually learning more about it through your use.

The second message is that when you concretize algebra, when you and your students discuss its applications or when you discuss it at all, you are transporting them to the land of algebra in order to make them more fluent in the language. But if you just treat the subject abstractly, without context, then you are acting as if algebra is a dead language and there is no land to which you can now transport your students.

The third message is that students must learn how to use today’s technology, just as they learned how to use yesterday’s. Yesterday’s technology included the use of tables for squares and square roots, logarithms, and trigonometric functions, and all sorts of algorithms for rewriting expressions and solving equations and inequalities. Today’s calcularots and computers incorporate the tables and have new algorithms. Yesterday’s technology is much more difficult to use than today’s, but today’s is not trivial. It too has to be taught.

Today’s symbol manipulator technology acts like a language dictionary. It tells which expressions mean the same thing. It indicates synonyms for complicated expressions, and because we are dealing with mathematics, you have the opportunity to show how one creates synonyms. Learning a foreign language is very difficult if you have no dictionary, because people keep using words you do not understand and because you are always unsure of how certain words are spelled. Likewise, the technology will help students learn algebra. The interesting outcome from having the new technology is that our courses become simultaneously both more conceptual and more applied.

There will be teachers who don’t want their students to have the technology. They will say that the student no longer has to work or no longer has to think. They do not understand that the purpose of teaching a language such as algebra is so that students can communicate, reason, and problem solve in that language, not so that they can find synonyms or learn to spell. Students should not have to look up every word in the dictionary, but they must learn how to use the dictionary.

The fourth message is that the previous messages also apply to the learning of calculus. When we teach inequalities, distance, area, rate, infinite decimals, slope, sequences, functions, limits, summation notation, maximum or minimum problems, we are engaged in the first stages of the learning of calculus. We should not shy away from making the connections, because the learning of calculus also requires many years for its fluency. And we must use the technology.

The fifth and last message is that these new developments, make it reasonable to believe that the ideas of algebra and calculus can be learned by virtually all students. But no person will believe that these ideas should be learned by all students unless he or she is convinced that the subject is important enough to warrant such a hallowed position in the schooling of students. Both the natural universe and that part that has been made by humankind may be written in the language of mathematics, but if we mathematics teachers do not teach the connections to that universe, we cannot expect others to do it for us. The developments of the last generation are a challenge to all of us, but they make the teaching of mathematics in this generation as exciting as it ever has been.

We hope that at this conference you will have many questions answered and gain many ideas that will help you and your students capture this excitement and gain fluency in the language of mathematics. Please let us know if there is anything more we can do to help you.

Contact

UCSMP
1427 East 60th Street
Chicago, IL 60637
T: 773-702-1130
F: 773-834-4665
ucsmp@uchicago.edu