Paper-and-Pencil Skills in a Calculator/Computer Age
Presented November 12 & 13, 1994
UCSMP Director Zalman Usiskin presented this talk at the Tenth Annual UCSMP Secondary Conference, held November 12 & 13, 1994. It has been edited slightly for publication. This article was published in UCSMP Newsletter No. 16: Winter 1995.
Introduction
The construction of the mathematics curriculum is a complex process. A balance must be struck between generalizations and specifics; between routine, nonroutine, and partially routine questions; between skills, properties, uses, and representations; between open-ended and finite tasks. This content must be selected from an overwhelming array of potential concepts, algorithms, and problems, from arithmetic, statistics, algebra, geometry, discrete mathematics, and analysis. The content must be sequenced, and we must decide whether to begin a lesson with a skill, an application, a concrete representation, or a general property, whether we should move in a logical sequence, or a sequence stemming from solving a problem, or from the history of the idea, or based on psychological theory. And we must take into consideration the vast differences among our students: from those who already know most of what we plan to teach to those who have no clue; from those who are diligent workers to those who are negligent workers; from those who have resources and can get help whenever they need it to those who live in less-than-favorable conditions with no home support.
There are corresponding differences among teachers that determine how that curriculum is delivered to students: from teachers who use cooperative learning everyday to those who never use it; from those who love calculators and bring classes to computer labs to those who only recently and reluctantly have allowed calculators in their classroom; from those who are into writing and alternate assessment to those who are hoping these are fads that will blow over.
In the 12 years of UCSMP, surely the most salient and ubiquitous of the curriculum issues has been the role of paper-and-pencil skills in an age of increasing use of calculators and computers. As you probably know, from the start of UCSMP we required calculators in all our courses; we were the first secondary curriculum to do so. We required computers in one of our courses before there were user-friendly graphing calculators and we continue to believe it is important that students see what powerful machines can do in mathematics. We were the first to eliminate certain paper-and-pencil skills from both our algebra courses. But we still include in our courses a considerable amount of work with paper-and-pencil skills.
The origins of my remarks today date back to the middle 1970s, when hand-held calculators were first appearing in schools and Max Bell and I were asked by Marilyn Suydam and Dick Shumway at Ohio State to write a position paper regarding the implications that calculators would have for school arithmetic.
Since that time, there has been a revolution in technology. Paper-and-pencil graphing in algebra and statistics, and paper-and-pencil drawing in geometry can now be done with relatively inexpensive and user-friendly technology. Paper-and-pencil algebraic skills can now be done with a little more expensive and a little less friendly technology, but then, these skills have always taken a little more time and have always been a little less friendly.
There is no sign that the progress in technology is likely to diminish. Hand-held devices are now far more powerful than the first Apples, and they continue to become still more powerful.
Despite these advances, some people still resist the use of technology to replace paper and pencil methods. While it is common for those who favor technology to dismiss paper-and-pencil zealots as being out of step with the times, this resistance is not always caused by such reasons as "What will they do if the batteries run out?" or "They need to know the skills for the test." The beliefs run deeper than that, and are held by some of our best schoolteachers and many mathematicians. So in this year's talk, I decided to reexamine the role of paper and pencil skills in school mathematics in a technological era.
Types of Algorithms
Paper-and-pencil work in mathematics begins in kindergarten when children learn how to write numerals. This work proceeds through school with activities such as taking notes, writing steps of algorithms, recording solutions to problems, and drawing figures; and continues through life, with the recording and processing of information such as in checkbooks, or the writing of reports. Some of this paper & pencil work we call "skills". The particular paper-and-pencil skills I wish to focus on are those associated with algorithms. Here I use the word "algorithm" in its usual way, as a step-by-step procedure for accomplishing a task that we desire to accomplish.
There are a great many paper-and-pencil algorithms in school mathematics. Sometimes we describe them by the task they accomplish — for instance, we may speak of algorithms for dividing fractions. Sometimes we describe them by individual names — e.g., when we speak of long division we mean a particular algorithm written down in a particular way. In preparing this talk, I found it impossible to stick to one of these types of descriptions. But I think it is convenient, to sort these algorithms into three categories:
Arithmetic algorithms, such as cube root, square root, long division, long multiplication, column addition, subtraction with many digits, division of fractions, addition of fractions, calculating the mean, standard deviation, etc.
Algebra/Calculus algorithms, such as the solving of linear equations and inequalities, completing the square, partial fractions, calculating definite integrals, evaluation of formulas, logarithms for computation, simpification of radicals, lines and curves of best fit, calculating definite integrals.
Drawing algorithms, such as those for making bar graphs, circle graphs, coordinate graphs, the graphs of functions and relations, the ruler-and-compass constructions in geometry, the finding of transformation images of figures.
This sorting reflects the different kinds of technology that are commonly available as alternates to paper and pencil. I have tried to pick my examples from these three categories.
In the short time available, there are certain algorithms I cannot discuss: algorithms involved in memorized facts and mental mathematics; single-step algorithms, such as for the multiplication of fractions; step-by-step procedures used in certain types of proofs, such as in the proofs of formulas for certain sums using mathematical induction, or triangle congruence proofs.
Basic Principles About Teaching Algorithms
Let me begin with five principles that I believe we could all agree on. Some of us might even consider many or all of these principles to be truisms.
- Technology changes the relative importance of algorithms. Some algorithms become more important, some become less important, some do not change in importance.
This principle was one of the original beliefs underlying UCSMP.
- For a given task, algorithms involve three types of processes: those you do in your head, those you keep track of with paper and pencil, those you do with the aid of technology.
This is a principle reflected in many national reports. However, it is not as simple as it seems. Consider the multiplication of fractions in algebra, say as simple a question as to simplify (3/x) • x2. If we write down only the answer 3x, have we used paper and pencil or done it in our heads? It isn't a basic fact, but we may have done it all mentally, imaging the paper-and-pencil work (3/x) • x2 = 3 • (x2/x) = 3x.
- No matter what algorithm you think you are teaching, students will process it in different ways.
This is the constructivist paradigm. Some who call themselves constructivists have interpreted this as then assuming one should not teach algorithms at all because it is senseless to teach something everyone will interpret differently. They believe children should invent all their own algorithms. If we were to take that argument to its extreme, then we would have to accept that we should not teach anything, because clearly everyone processes all information differently. It would also mean that children should discover all knowledge, which is impossible.
We learned in the 1960s, with all the studies on discovery teaching, that it is good to have children discover. But we also learned that they cannot discover everything. Not only does it take too much time, but much in mathematics of what is taught is too hard to be discovered by students without great guidance; it can only be discovered if the teacher leads the students step by step to the discovery; it then is usually no longer discovery but guessing where the teacher is going. I believe that, except for the simplest algorithms, it is expecting too much of students to expect them to adapt algorithms.
- In order to use an algorithm, you must have the necessary tools for that algorithm and you must know how to use the tools to carry it out.
- To be worth teaching, an algorithm must have a purpose.
Common purposes of algorithms in school mathematics are to get an answer, or to find an equivalent expression or draw a picture that makes things easier, or clearer, or simpler, or takes less space.
There are algorithms with no purpose. For instance, why rewrite
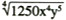 as
as 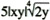 ? Is this a better form for later use? Does it help understanding of anything? Does it take less space? It has little if any purpose, so any algorithm for it is not worth teaching.
? Is this a better form for later use? Does it help understanding of anything? Does it take less space? It has little if any purpose, so any algorithm for it is not worth teaching. - Blind acceptance of results.
Because an algorithm is supposed to be automatic, and done quickly and efficiently, answers are often blindly accepted. This is true regardless of whether one does the process mentally, with paper and pencil, or with technology. This is the reason that in UCSMP texts we present checks for problems as often as we can. We want students to have at least two ways to get an answer to a question. Checks are necessary for all procedures, whether they have taken a long time to obtain or have been obtained quickly.
- Overzealous application.
Because the best algorithms are powerful in the sense that they can be widely applied, there has always been the tendency for students to overapply them, to use an algorithm for something that could be done mentally. We have all seen students do something like the following:
345 X 10000 000 000 000 000 345 3450000or
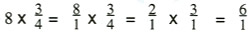
(and then not realize that the answer is 6)
or
or, use long division to rewrite 37/2 as a decimal. And we all see students use calculators to do arithmetic that they should do in their heads.
These overzealous applications of algorithms are not wrong mathematics, for the students are playing things safe, worried about losing accuracy if they deviate from an algorithm for a simple special case. They may be unwise and inefficient, but they are not wrong. In this regard, perhaps the most common story told to me by older adults is that they are astonished that cashiers can no longer give change without having the cash register do it for them. I have never seen a study of this and wonder how true it is, but I can tell you that I would rather the cashier have an automatic way to give me change; I trust the machine more than I trust the cashier. And both the cashier and the cashier's boss are probably correct to require that the machine be used whenever possible.
In this regard, mental mathematics can be as dangerous as paper and pencil or calculator. With mental arithmetic, we don't even know whether the input was correct.
- Belief that algorithms train the mind.
There are some who claim that doing the paper-and-pencil algorithms trains the mind in good ways, that going through these procedures teaches orderliness and care. There has never been any evidence of this. Even mathematicians, who tend to be better at these algorithms than other people, are no more orderly than other people. We know this; we have all taken classes from them.
The evidence is, in fact, to the contrary. These algorithms seem to take students' minds off of the bigger picture, and turn many students off towards mathematics. These cartoons ("The human brain starts working the moment you're born, and it doesn't stop until you get to long division." "Son, I want you to feel as if you could ask me about anything — except how to do synthetic division of polynomials.") state the point eloquently.
It is true that the idea of an algorithm is an important one — that people do need to follow directions in many life activities. The learning of mathematics may contribute to this, but probably no more than other subjects in school.
- Helplessness if the technology for the algorithm is not available.
Both paper-and-pencil algorithms and calculator/computer algorithms require the user to have some equipment. Proponents of paper and pencil have often argued that paper and pencil is more likely to be available than calculators or computers, but today there are times when the reverse is true: as I said earlier, when schools are out of paper but computers are available; when all the pencil points are broken and the sharpener is out of commission but a calculator is available; when one needs quick computations and it is far easier to take a tiny calculator out of one's wallet to do them than to take a pencil and note pad out of one's pocket or purse.
- power
- reliability
- accuracy
- speed
- record provided
- mental image
- instructiveness
- use in later algorithms
- objects of discussion
It follows that we cannot expect students to use paper-and-pencil algorithms if they do not have paper and pencils. This is, in fact, the case in some schools, where it is typical to have a shortage of paper by the end of the year. It also is the case with some students, who may have notebook paper but do not have plain paper or graph paper when that would be more appropriate, or who do not have a sharpened pencil. Every classroom in which students are expected to use pencils should have an automatic sharpener. I'm amazed that there are classrooms in which there are computers but no automatic sharpeners.
For calculators and computers, this principle implies that we can't avoid teaching a topic just because people these days do these tasks with calculators or computers. If the task is important, we are obligated to teach students how to use technology to do it. But we cannot expect students to use that technology unless it is readily available to them at all times. Consequently, the cost of technology plays a significant role in the choice of algorithms.
Reasons for Algorithms
Why don't we just let students locate algorithms in reference materials, or invent their own algorithms as they need them? We teach algorithms because there are important reasons for teaching them. These reasons also provide ways to decide which algorithms to teach.
Power
Algorithms are generalizations that embody one of the main reasons for studying mathematics — to find ways of solving classes of problems. Algorithms solve classes of problems, not just single problems. They guarantee an answer or answers. They complete a task.
The power of some algorithms is easy to determine. The Quadratic Formula gives solutions for all quadratics, even those with coefficients that are not real numbers. The use of the Law of Cosines to find the third side of a triangle given SAS works on all triangles. Long division has power; it can be used with decimals having any number of digits. Simply using the ÷ "divide" key on a calculator does not have as much power, for its use is limited to the number of digits in the divisor, dividend, and quotient that the calculator can hold or display. Can you use a calculator if you want to divide by a 15-digit number? Not easily with most calculators I know. But I could do 15-digit long division with paper and pencil.
Does this mean that I should teach long division with that many digits? Not necessarily — remember that an algorithm must have a purpose, and if one never has to divide by numbers with 15 digits, then there is no purpose in learning an algorithm for that task. And even if one did have to do this kind of division, there are computer algebra programs.
Reliability
When an algorithm is done correctly, it is reliable. It gives the correct answer. The importance of reliability is obvious. But if there is a possibility of error in the carrying out of an algorithm, then the algorithm loses some of its reliability. So the difficulty of carrying out the steps in an algorithm without an error is something that has to be taken into account when examining it, and is one of the reasons that we tend to prefer computer or calculator algorithms over paper and pencil.
Accuracy
The better algorithms are more accurate, and they may also tell you how accurate the answer is.
This is why we are usually not satisfied with an estimate when an algorithm for an exact answer is available. You know what happens when you ask students to estimate 51 X 39 without any context or real-world situation. Some students will multiply the two numbers, get 1989, and give you that as an estimate. You may think they've missed the boat, but in fact they have merely given you the best estimate they can. Similarly, if we wish to know where a parabola intersects the x-axis, we usually prefer solving a quadratic equation to examining the graph to find an estimate. The SOLVE key on some calculators can do this automatically, but the estimate it gives is not as satisfying as an exact answer. This may also be why we often prefer answers like 10π to 31.416. A good algorithm allows us to get virtually as accurate as we wish.
Speed
An algorithm enables a direct route to the answer rather than blind alleys. The better algorithms are faster than poorer algorithms. Another sense of speed is the ease with which the algorithm is learned or recalled. An algorithm that is fast but that is difficult to remember is not necessarily a good algorithm. For instance, consider the formula for the inverse of a 2 x 2 matrix.
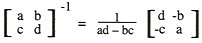
This formula gives an algorithm for obtaining that inverse. Just substitute. Since the formula is reasonably simple, the algorithm is fast. But it's a tricky formula, and many people forget it. The algorithm is of no use if it is easily forgotten.
Record
Paper-and-pencil work, calculator key sequences, and computer programs provide a record of the algorithm that was used to determine the answer. The record of an algorithm is significant for teaching because we often want students to examine the process by which students obtain their answers, and we want students to share with each other what they have done, to refine their procedures. This record also allows us more easily to locate errors in doing the algorithm.
Mental Image
The written record also produces a mental image that can be used for doing things without paper and pencil. For instance, suppose I drive 412 miles and use 15.4 gallons, and I want miles per gallon. Then to divide 412 by 15.4 in my head, I mentally picture the long division algorithm, placing 308 under the 412, recording 2, and subtracting. Now I look at 104, divide 1040 by 15.4 in my head, obtaining 6. This gets me about 26 miles per gallon, and in fact I know that the remainder is about 2/3 of the divisor, so I estimate 26.6. I am very good at mental arithmetic, and I know that part of my skill at that is because I can picture the algorithms in my mind. I do this with algebra, also. If I wish to solve 8x — 14 = 6x + 88, I subtract 6x from each side and then I add 14 to each side. I get 2x = 102, from which x = 51. My mental method is clearly derived from the paper-and-pencil method I was taught.
Instructiveness
Some algorithms shed insight into the relationship between the answer and the given information. For instance, the algorithm used for adding columns of numbers, in which one records a "carry" digit somewhere, is instructive in that it shows the place value ideas that are used. The multiplication of polynomials in algebra is also instructive — we can identify a clear use of the distributive property, for instance, when we show the middle step in
(a — b)(a + b) = a2 — ba + ab — b2 = a2 — b2.
In these situations, the paper-and-pencil algorithm provides not only a method for getting a result, but also a proof of the result or a sketch of a proof. The paper-and-pencil algorithm hasn't merely announced the result; it has constructed it.
Although algorithms on calculators may bypass some intermediate steps, because of speed they can show patterns between given and answer that are unattainable or hard to see when using paper-and-pencil. For instance, you can change factors and see changes in products; you can change coefficients of equations and see the effects on the solutions; you can change inputs into graphs and see the changes in the graphs; you can transform geometric figures and compare the images with each other or with the given figure.
Proof
More algorithms constitute proofs than we usually acknowledge. For example, consider the sentence 30 + .41m > 50, which could arise if you were given two choices for renting a car, either $30 a day and 41¢ a mile, or $50 a day with unlimited mileage, and you wondered when the first choice is more expensive. Here m is a number of miles, which for the purposes of computation of cost, is rounded up to the nearest integer. How we record the algorithm is critical. Here is one way.
30 + .41m > 50
.41m > 20
m > (20/.41) = 48.78...
m > 48
Do you think this is enough for a proof? I can put in more steps which make the movement from one step to the next rather obvious, but these extra steps disconnect the given from the solution.
30 + .41m > 50
30 + .41m — 30 > 50 — 30
.41m > 20
(.41m/.41) > (20/.41)
m > (20/.41) = 48.78...
m > 48
Adding more steps does clarify what is done in the algorithm — it clarifies the proof, but it makes it more difficult to see the relationship between the given and the answer. By the time we go through all of these steps, the student may have forgotten what the question was about. As teachers, we know we need sometimes to put in more steps, sometimes to take out the steps. When the steps are easy, then they are easy to put in or take out; when the steps in an algorithm are difficult, we may wish to omit them always or almost always.
We combine algorithm and proof often in geometry, with the ruler and compass construction of an equilateral triangle.
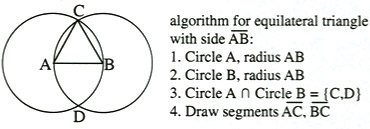
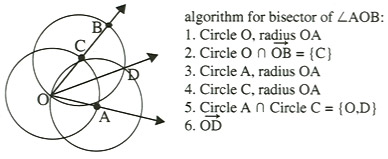
This construction is instructive; it elegantly exhibits not only the equilateral triangle but also its reason for being equilateral. On the other hand, the ruler and compass construction of an angle bisector is not very instructive; it does not so closely resemble a proof; it is more instructive simply to measure half the angle and draw an appropriate ray.
Use in Later Algorithms
An algorithm in one situation may be part of a larger algorithm in another situation; thus certain algorithms can be more important than others. Long division is often justified because division of polynomials follows the same form. Addition and subtraction of positive and negative numbers are needed for solving linear equations. The drawing of a parallelogram is needed for the drawing of a cube. The graphing and tracing of a function is needed if we wish to use the graph to estimate a maximum point or solution to an equation.
Objects of Study
Algorithms can be objects of study. We can compare their efficiencies, their mathematical characteristics; and their speed. We include some of these ideas in the UCSMP course Precalculus and Discrete Mathematics. However, we have in UCSMP texts not chosen algorithms for use by students because they are interesting to study, though we often discuss and compare algorithms with each other in an informal way.
Dangers Inherent in All Algorithms
There are dangers inherent in all algorithms, whether paper and pencil or computer/calculator.
Selecting Among Available Algorithms — Paper and Pencil, or Calculator/Computer?
When there is more than one algorithm with sufficient power to complete a particular task, the algorithm of choice is normally the faster, or the more accurate, or the more reliable. Indeed, speed, accuracy, and reliability are ultimate goals for almost all algorithms of any importance. On these dimensions, many paper-and-pencil algorithms are undeniably poor compared to technology, and account for the use of technology rather than paper and pencil by adults as consumers, at play, and in the workplace. The speed of calculators and computers also frees up time in the classroom to study the other dimensions of mathematical understanding — the properties, uses, and representations; to discuss many aspects of problem solving: the relationships of problems to each other, the various ways they can be solved. The speed, accuracy, and reliability allow students to see patterns between problem and solution they might not normally be able to see, and to explore these relationships. Furthermore, because technology often allows us to go directly from given to result, the intermediate steps do not get in the way. For instance, we do not have to spend time plotting points to see how the equations and graphs of functions might be related.
Although there is not time to go through the entire curriculum, I thought it would be instructive to give a number of examples of how we at UCSMP have made decisions regarding which algorithm to use for accomplishing a particular task. It helps to keep in mind the reasons mentioned earlier for algorithms.
These criteria apply in comparing any two algorithms with each other, but for the present let's be simplistic and compare paper-and-pencil to calculator/computer algorithms as if there is only one of each type. There are then only four possibilities, as given by this matrix multiplication diagram, where the Ys and Ns stand for yesses and nos.
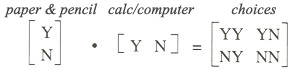
YY: Teach both paper-and-pencil and calculator/computer algorithms.
The safest decision to make is to desire to have students learn all the algorithms, both paper-and-pencil and calculator or computer. We have done that in our texts with such things as operations with fractions. Because fractions represent division in standard algebraic notation, algorithms with arithmetic fractions are applicable also with variables. In this regard, algorithms with fractions are relatively more important than algorithms with decimals. They are used in the solving of equations such as ax = b or f(2,3)y = 10 or πr2 = 100 or the rewriting of 3x + 4y = 12 in slope-intercept form. Consequently, a decision not to give students paper-and-pencil work with fractions means it is more difficult for these students to do later algebraic work with paper and pencil. Consequently, we teach the paper-and-pencil algorithm even though we know that students may have calculators that operate on fractions.
With most drawing, we also feel that students should be able to draw both with paper-and-pencil and with the aid of technology.
With some graphing, we also teach both kinds of algorithms. We think that the paper-and-pencil process of graphing a line is quite instructive and also accurate, and that the need to draw a scale in this, the first experience graphing an equation, is important to emphasize. Furthermore, to some extent the hand graphing of all equations and functions is more or less the same, and so this paper-and-pencil algorithm does not have to be taught again. But after this graphing of lines, we want automatic graphers to be present because of their speed, accuracy, and reliability.
YN: Teach only paper-and-pencil algorithms
Every paper-and-pencil algorithm can be programmed to be done by a computer. So when we teach only paper-and-pencil, it is never because we could not perform the task with technology. It is only when the technology is so cumbersome to use that it does not give us speed, or is too costly to expect students to purchase it, that we cannot assume its use.
Calculator and computer technology is available for solving all equations symbolically. Even if you have not used this technology, called symbol manipulator technology, you may know its names: Mathematica, Derive, and Maple are the most common computer programs, and the HP calculators do symbolic manipulation. This software is reliable, accurate, fast, and powerful; the HPs, however, are very difficult to use. The software can be instructed to go through steps, so it can provide a record as thorough as any paper-and-pencil record. But those steps are not easy to use, the technology is not yet cheap, and so we made the decision that we would not teach these calculator or computer algorithms.
When symbol manipulators become widely available, we will probably take the same view with equation-solving that we do with graphing. That is, we will continue to teach students paper-and-pencil means for solving linear equations, because the idea is important and the process is generalizable. But we will show how to use symbol manipulators to solve these and also more complicated equations. These algorithms will move from the right hand column YN and NN to the left hand column YY and NY.
NY: Teach only calculator/computer algorithms
Sometimes we have ignored paper-and-pencil algorithms, even when they are not difficult. With decimal arithmetic, we decided to assume calculators and not reteach any paper-and-pencil algorithms, even those paper-and-pencil algorithms we consider important. We want students to be able to add and subtract decimals by hand, but we feel they should have learned this before starting Transition Mathematics. In making this decision, we applied a substantial amount of research that showed that time spent on these algorithms at the 7th grade level or higher tended merely to put students further behind rather than to get them ahead.
It is the case that every calculator or computer program could also be done by paper and pencil, but some paper-and-pencil methods are so unwieldy that they give neither speed nor accuracy. Then we may teach only the calculator/computer algorithms. For instance, we teach students how to estimate the solutions to numerical equations in one variable with a graphing calculator, by tracing on graphs. These calculator algorithms are reliable, fast, provide a mental image, and are instructive, and are so powerful that they can be employed on 5th degree polynomial equations, or sin x = log 3x — 5, or many others for which there is no known paper-and-pencil algorithm that gives an exact solution. Their only drawback is that they do not give exact solutions. But even this drawback can be turned into an advantage, because it motivates us to ask when we can get exact solutions, and to examine such equations more closely.
For the graphing of complicated functions, the accuracy, speed, and reliability of automatic graphers overwhelms that of paper-and-pencil methods. In fact, the best paper-and-pencil methods for many functions require calculus and so are out of the reach of our students. So we assume that students have automatic graphers like the TA-81 or TI-82 always available, and we never use paper-and-pencil methods on them.
For these same reasons, we teach only the calculator/computer algorithm for obtaining a line or other curve of best fit. For estimating nth roots or calculating nth powers or doing all sorts of complicated arithmetic, we completely ignore the paper-and-pencil methods, most of which require logarithms, we rely completely on the more accurate, faster, and powerful calculator algorithms.
NN: Teach neither type of algorithm
When the task is not important enough, then it does not belong in the curriculum. This is obvious enough, but importance itself changes; a task that is not important one year may be important at some other time. For instance, operations with rational polynomial expressions are not important enough to be in UCSMP Algebra or Advanced Algebra, because there are more important things all students should know. But, for a variety of reasons, calculus requires that students be familiar with rational functions, and in Precalculus and Discrete Mathematics, where these functions are discussed, it is suitable to discuss the corresponding manipulations.
There are actually very few problems that were in the curricula of yesteryear that are not somewhere in the UCSMP curriculum. Though paper-and-pencil algorithms such as Cramer's Rule for solving systems; the hand calculation of square roots; the use of logarithms for computation with trig functions or with complicated arithmetic, the drawing of a triangle given the lengths of some combination of sides, medians, or altitudes; complex manipulations with radicals and with rational expressions are not in our books, the problems for which these algorithms were designed remain. Today's students are able to do calculations, solve equations, graph functions, and draw figures that students even 25 years ago could not dream of doing without extraordinary effort, and the fact that we have four years after algebra and before sustained study of calculus in our curriculum means that we can discuss statistics and discrete mathematics and we don't have to get rid of these problems.
If we look back at the 2 by 2 matrix of yesses and nos, we see that we are in a time of change, in which there is a noticeable shift almost year by year to the left — to the use of a calculator or computer. There is also a shift down — though this may not be as dramatic a shift — to not teaching as many paper-and-pencil algorithms. We also see that it is almost certain that we will always have some entries in the upper left, tasks for which we teach both paper-and-pencil and calculator or computer algorithms.
How can we be so sure of the future in this regard? It's not so difficult. Keep in mind that when paper-and-pencil algorithms were introduced — mostly about 400-500 years ago — they constituted the advanced technology of their time. Paper was not widely available like it is today, and the writing implements of the time were much more difficult to use than today's pens and pencils. These algorithms were not immediately accepted by all because some people feared a loss of mental power that would come with algorithms that enabled you to do mathematics without as much mental arithmetic and other mental work. Yet, even though paper-and-pencil algorithms ultimately triumphed and became used for almost all of mathematics, still one was expected to memorize certain facts and formulas. The old ways did not die out completely because it was not efficient to have to recall or reconstruct or even write mathematics every time you needed it. And so we can expect, that although calculator and computer algorithms will overtake virtually all paper-and-pencil algorithms, a few of these old algorithms will remain. Those that remain will be in our curriculum not because they are curiosities and not because they train the mind, but because they provide some of the qualities that good algorithms provide.
Two Closing Thoughts
Those of you who follow these yearly addresses may remember that two years ago I chose to talk about what changes should be made for the second edition of the NCTM Standards. I praised the writers of the Standards for conceptualizing three facets of mathematics that lead the list of curriculum standards at each grade level: problem solving, communication, and reasoning. But I thought that a fourth facet, "procedures", was missing, and that there needed to be detailed discussion of this important aspect of mathematics. It did not dawn on me until after I had written the first draft of this talk that my remarks today could be interpreted as an elaboration of those remarks of two years ago.
These four facets of mathematics — procedures, reasoning, problem solving, and communication — remind us continually of the breadth and wide-ranging importance of mathematics. They are somewhat related to the four dimensions of understanding that we emphasize in UCSMP materials — skills, properties, uses, and representations. These categorizations reflect the belief that procedures are important, but they constitute only a part of mathematics. Procedures are a means by which we solve problems, by which we explore and represent relationships, and through which we can explain to each other how we have arrived at conclusions. They are not the ends of mathematics, but mathematics cannot be done without them. Because of this, we need careful discussion of procedures, and I hope that my remarks today contribute to that discussion.
Contact
UCSMP
1427 East 60th Street
Chicago, IL 60637
T: 773-702-1130
F: 773-834-4665
ucsmp@uchicago.edu