Individual Differences in the Teaching and Learning of Mathematics
Presented November 13 & 14, 1993
UCSMP Director Zalman Usiskin presented this talk at the Ninth Annual UCSMP Secondary Conference, held November 13 & 14, 1993. This talk has been edited slightly for publication. This article was published in UCSMP Newsletter No. 14: Winter 1994.
My remarks today relate to one of the major changes in thinking in school mathematics since the inception of UCSMP ten years ago. In 1983, the report A Nation at Risk recommended a two-tiered system for the teaching of mathematics in high school. This was not unusual for the time. Here is what it said.
The teaching of mathematics in high school should equip graduates to: (a) understand geometric and algebraic concepts; (b) understand elementary probability and statistics; (c) apply mathematics in everyday situations; and (d) estimate, approximate, measure, and test the accuracy of their calculations. In addition to the traditional sequence of studies available for college-bound students, new, equally demanding mathematics curricula need to be developed for those who do not plan to continue their formal education immediately. (National Commission on Excellence in Education, 1983)
The first part of this recommendation has been accepted in many quarters. But not the second part. The “new equally demanding mathematics curricula" for non–college-bound students, at least as far as meeting graduation requirements, are increasingly the same courses as for college-bound students.
We at UCSMP have contributed to some of these changes. Many students using UCSMP texts tend to take algebra and geometry a year earlier than used to be the norm, and many go on to take more mathematics than they would have before. Because of these developments, every teacher is being asked to accommodate a wider range of students in each class, and yet, more than ever, to recognize and deal with the differences among students.
The difficulty this presents is that though many children learn mathematics in much the same way, there are also patterns in the learning of mathematics that are unique to every person.
Anyone who creates curriculum, and anyone who teaches more than one learner at a time, must face the dilemma caused by these differences among our students. When do we put learners through the same experiences? When are the differences enough to warrant separate modes of instruction in the same class? When do the differences warrant separate courses?
In 1983 it was common to have multiple courses in every grade. In 7th grade, two courses, usually pre-algebra for the best and a standard 7th grade for the rest. In 8th grade, two or three courses: algebra, a standard 8th grade, and a remedial course. In 9th grade, larger high schools might have four or more courses: geometry, honors algebra, regular algebra, a two-year or pre-algebra, and general mathematics. Sometimes general mathematics was the second course in a sequence of basic mathematics, general mathematics, and consumer mathematics taken by 9th through 11th graders. Three levels of geometry and two or three levels of advanced algebra were common. So were two or three levels of senior mathematics, if advanced placement is included. The sum total of all this is that a junior high school might offer six different courses in grades 7 and 8, and a senior high school of 2000 students might have more than 15 separate mathematics courses.
These practices have always created difficulties for schools. It is havoc to schedule students into courses with a small number of sections. The more levels there are, the more likely one is to make mistakes in placing students. And can students move from level to level? Furthermore, there is an undemocratic aspect to levels, in the sense that they deprive students of equal opportunity. Finally, we have learned that the lower levels do not remediate most students, but tend to place them farther behind their classmates.
Faced with these arguments, we justify our various offerings by noting how difficult it is to teach a wide range of students at a given level. Yet mathematics is just about the only subject in which there are all these levels. Why are teachers of other subjects able to deal with such differences, but not we in mathematics?
Individual Differences in Ability
Despite all our experience with student learning and despite huge amounts of research, we know virtually nothing about the ability of people to learn anything, let alone mathematics, because we still know very little about how the brain operates. We do know that a single number like the IQ does not serve us well.
How complex are the relationships among abilities? A metaanalysis of variables that correlate with mathematics scores done by Lynn Friedman a few years ago showed the surprising result that reading comprehension was more strongly correlated with geometry performance than spatial scores. In retrospect this may not be too surprising: language ability is surely strongly correlated with mathematics ability because mathematics is very much a language.
However, one must be careful when using test scores or correlations among test scores to make an argument about ability. Some people still think girls differ from boys in mathematical ability, and they use test scores particularly among the highest performing students and the very small number of female mathematicians of top rank to make their arguments. And some minority groups score significantly lower than the rest of the population. Yet we know that those differences are not due to differences in ability.
But our lack of knowledge about what constitutes mathematics ability does not keep people from making decisions about students based upon supposed differences in ability. Judging from what we do in school, there are a number of theories about how individuals differ in ability to learn mathematics. Each can be described by a reasonably simple mathematical model.
The most common mathematical model of ability is the normal distribution.

Many of us have been taught to think of ability using this curve, and virtually all standardized test scores are fit to it. IQs and SATs are fitted to this curve. When we give tests, we often get a normal distribution. But mathematically, this distribution is forced on us not because of differences in student ability, but because too often tests contain many questions of a similar, low difficulty, and so we get the sum of rather similar binomial distributions, and that sum is a normal distribution. We would get the same normal distribution if each student was a six-sided die and we tossed the dice for all our students and added the results to get our grades.
However, heights of people from the same gene pool and many other characteristics are normally distributed. So the normal distribution is not necessarily the wrong model. If we assume that ability is actually distributed this way, and if we differentiate students because of their scores, we must draw vertical lines in the graph. I’ve drawn them at about one standard deviation from the mean, so that about 16% is on the right and left; this is essentially where many schools draw the lines between "regular" and "honors" students to the right, and regular and "remedial" students to the left.
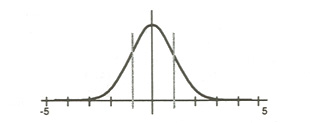
The problem is that when we separate students in this way, and give those to the right — the top scorers — opportunities to learn everything the other students learn and even more, and give those to the left — the bottom scorers — fewer opportunities, then we have implicitly applied a different model of ability, the broken normal.
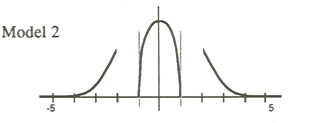
This model represents the belief that most students can learn a fair amount of mathematics. But some simply cannot learn what others can. And some are special and can learn much more than average students. I think many people today believe in this model. When we teach the students in these groups different mathematics, we wind up with three overlapping normal distributions. It makes us think that students are more different than they are.
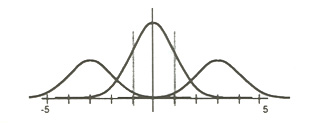
Let me return to the original normal distribution. Maybe the distribution is normal, but not so wide.
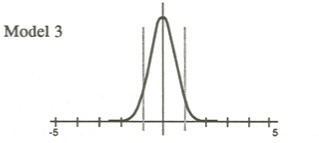
Now virtually all scores fall between those same vertical lines that split the students in the first place. This would argue for placing almost all students in the same classes.
Of course, everyone knows that mathematics ability involves many different aspects of a person, so a one-dimensional model, like the normal distribution, is not complex enough. Some people, reacting to our current state of ignorance, implictly assume what I call the discrete n-space model of ability. One thinks of students as being independent but possibly overlapping spheres. That is, they all have different abilities, and sometimes these abilities overlap.
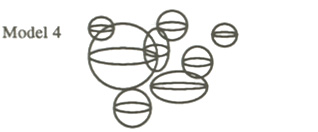
In this model, we give all students the same instruction because we do not know who will benefit most. The spheres are multidimensional, but no one knows how many dimensions!
In the context of schooling, this is a discrete dynamical system model. The initial value is the aptitude of our students as they come to us; the iterated function is the effects of our continued instruction. It is a chaotic model in the sense that students whose spheres are near each other might benefit quite differently even from the same instruction.
Which model is correct? If we were trying to get students to perform to the limits of their ability, then I think there might be some reason to believe that differences in ability are significant enough to cause severe limitations on what students could assimilate. Then a model such as the first normal distribution might be reasonable. But we know that students in other countries are given and succeed with a more ambitious curriculum than we have in the U.S. in the past offered. The enormous similarities that are found in class after class, student after student, lead me to believe that student ability to learn mathematics is not as haphazard as the discrete dynamical system model would suggest. And I do not believe that mathematical ability is something you either have or don’t have, so the broken normal distribution does not fit either. This leaves only a model in which all students are reasonably alike in ability, somewhat like a squeezed thin normal distribution.
1. Individual differences in ability are not great enough to warrant differences in curriculum, except in unusual circumstances such as major learning disability or extraordinary talent.
The sense of the word ability in this principle is innate ability or limitations on learning mathematics. A different use of the word ability is in the sense of ability to learn a particular course. That ability depends a great deal on entering knowledge.
Individual Differences in Entering Knowledge
In our studies of UCSMP texts, and in earlier studies we conducted here at the University, we found, as every other person who has ever tested curriculum has found, that — given equal opportunity to learn — entering knowledge accounts for from 30% to a little over 50% of the variance in student performance at the end of the year. No other variable accounts for anything close to this.
To account for the growth in students' knowledge over time, we must look at the entire process differently. With ability, we looked at the student as fixed and the mathematics as varying — we say that this or that mathematics can be learned by a student. When we think of the effects of entering knowledge, we have to view the world of mathematics as reasonably fixed, and the student as taking or being led down a path through that world. We might call this the path model of ability.

Here the world of mathematics is the inside of a sphere. This sphere has more than three dimensions, and it intersects other worlds of the student, so this drawing oversimplifies a very complex situation. Student paths intersect, overlap, and draw apart. At each point along the student’s path, some mathematics is experienced or learned. Students come to us from different paths, and at different positions along their paths. Instruction tends to bring paths together and can spur students to move more quickly and to traverse more paths, or it can serve to shut off opportunities to other paths. What the student can get to from a given point seems to me to be what the Russian psychologist Vygotsky has called the student’s zone of proximal development.
The UCSMP philosophy is that virtually every point in this world of mathematics is reachable by students, but they may get there through different paths and at different times. We try to construct our materials so that as many students as possible reach as many of the important or beautiful locations in this world of mathematics as possible.
This is the model we apply in our chart of who is ready for which of our courses when. (This chart can be found in the back of the teacher’s edition of any UCSMP text.) The significance of having students take the same courses but in different years is that a school may be able to get by with as few as ten different courses from grade 6 through grade 12, yet deal with the differences in entering knowledge of almost all of its students.
Differences in entering knowledge are very significant. In every course we have studied in a wide variety of school settings, we have had some classes with higher mean scores at the beginning of the year than other classes obtained at the end of the year, whether using UCSMP texts or using other texts. We all expect differences in student scores, but to have such differences in class means surely implies that we should be doing something different with each group. If two second-year algebra classes are such that one class enters with more knowledge than the other class will have at the end of the year, they need to be taught differently.
2. Individual differences in entering knowledge are great enough to warrant differences in what is offered to students at a particular grade level.
Why are there such great differences in students, if they are not due to ability? I think we have underestimated the degree to which elementary mathematics is a language. We speak of mathematics metaphorically as a language that describes the universe, but it may not be a metaphor. If mathematics is a language, then for children whose parents speak the language we should expect the same degree of differences in learning mathematics that we see between children in Germany and children in the United States in learning German. Children by 6th grade can be quite fluent in their native language. It may be no difference with mathematics.
We know that the key variable in learning new knowledge is opportunity to learn. Previous opportunities are usually what cause differences in entering knowledge. These opportunities occur both in and outside of school, and are analogous to the opportunities a child might have to learn a foreign language. When parents are familiar with mathematics, they share their knowledge by speaking the language. They use words like rectangle, graph, and percent, and they expect their children to be able to figure out what things cost and to read weather reports with understanding, to deal with taxes and discounts . Having a computer on which a child can work is a visit to the land where the language is spoken, because computers afford the possibility of immersion in virtually all of elementary mathematics. Surely one reason children of better educated parents do better in mathematics is because their parents are more likely to provide these opportunities.
In schools, the differences in opportunity to learn can be great even when there is no grouping. The elementary school child who has a teacher who does not like mathematics, or who teaches only arithmetic skills, can lose an entire year of mathematics just like that. The child with a teacher who spends 45 minutes on mathematics each day rather than 30 can gain a half year, just like that. The time available at the upper grades and in high schools averages from 40 to 55 minutes a day, and there is no question that teachers with the higher amounts of time to spend with their students can give students far more opportunities.
Individual Differences in Willingness to Work
As soon as there is significant homework, another variable affects what students learn. It is the amount of effort a student puts forth. The differences in willingness to work can be enormous, and there is no question that how hard students study one year affects the entering knowledge for the next year. Sometimes the student who works very hard, and who has support outside of school from parents or tutors, can overcome great deficiencies in entering knowledge from previous years..
Because it is possible to overcome differences with work, and because it is difficult to determine the ability of students, there has been a recent trend to do away with all grouping of students, even grouping based on entering knowledge. Transition Mathematics has been adopted in dozens, if not hundreds, of schools for all 7th grade students, or for all but the best, who have taken the course in 6th grade. In most of these places, by the middle of the year, the differences in entering knowledge and willingness to work cause schools to slow down the pace for some students, making the course either a year and a half or two years long.
Doing the course in a year and a half for some students seems quite sensible, but if the course has to be made two years long, then there should have been a course preceding it. It does not help students to move so slowly through a book that they get accustomed to a slow pace.
3. Individual differences in willingness to work are enough to overcome differences in entering knowledge and should be taken into consideration in any placement of students.
Now let us put principles two and three together. If a student enters a course with deficiencies in entering knowledge, and if that student is unwilling to work harder to catch up with classmates, then that student is very likely to leave the course with deficiencies. Yet we have some anecdotal evidence that students who perform even at the low C or D level in Transition Mathematics and UCSMP Algebra can succeed and become solid B students in later courses.
What seems particularly nonsensical to us are the senior high schools that force 8th grade UCSMP Algebra students to take algebra over again in 9th grade. With hundreds of schools having successfully implemented UCSMP Geometry in 9th grade, these schools are wasting an entire year by having students repeat algebra.
If it happens that UCSMP Algebra students are placed two years later in a second-year algebra course that emphasizes complicated manipulations that they have not had, they have to adjust. But such courses tend to be difficult for most students, and our anecdotal evidence is that UCSMP students do adjust, and rather quickly.
On the other hand, in some school districts that have adopted many years of UCSMP texts, we are beginning to see a very promising trend of teaching Transition Mathematics to greater numbers of 6th graders, and a few schools have begun to set a goal of having all 8th graders complete UCSMP Algebra.
We are looking forward with great anticipation to the completion of the UCSMP elementary curriculum in a few years. One goal of that curriculum is to have great numbers of students ready for a course like UCSMP Algebra in 7th grade. Certainly students coming through an enriched elementary experience can handle Transition Mathematics in 6th grade. In fact, though some may question whether 6th graders have the willingness to work and the maturity to sustain that willingness, our experience is that it is easier to start with high expectations early.
Individual Differences in Interest
Willingness to work is strongly related to interest, either in school generally or in mathematics particularly. Of course, willingness may be related to external factors, such as parental pressure or rewards, but we all know that interest based on internal motivation is a better variable in the long run.
Just as there are internal and external motivations for students to work, there are internal and external ways of creating interest in the mathematics classroom. We at UCSMP believe strongly that much of mathematics itself is interesting, that its structure and many of its results are beautiful, that there are important applications, and that the ways in which problems are solved in mathematics are often quite powerful with applicability outside mathematics. We do not have to make mathematics interesting for students; we have to bring out the many interesting aspects of mathematics. We have tried very hard to have our materials convey the many reasons why so many of us love the subject and why it is so important that students learn it.
The interests of students are probably best modeled by a discrete dynamical system of spheres like the one I showed earlier. Every student has a unique set of interests. For this reason, most students do not expect everything you teach to be of interest or of value to them. But they would like to know that every topic is of importance or interesting to someone and why.
Consequently, we try to vary the contexts of examples and questions. In FST and PDM, we have projects at the end of each chapter which provide an opportunity for students to spend more time in a particular area, and because of their popularity we are working to develop projects for all our courses.
But for some students this is not enough. Their interest cannot be satisfied in the confines of a standard class. They need more. They need activities outside the classroom, just as students who are very interested in sports or music do.
4. Every mathematics course should allow for individual differences in interest by including a wide variety of activities and contexts which bring out the brilliance, surprise, applicability, and structure of mathematics. Differences in interest in mathematics should be handled in classrooms via projects and other activities in which students are given choices, and, for those with great interest, outside the classroom via mathematics clubs and, for some, mathematics contests.
In many schools in which there are levels of the same course in the same year, the difference between the expectations for most students and the expectations for students in the honors classes are enormous. In these cases, teachers of the honors classes argue that the differences in interest and entering knowledge are so great that there is a need for the honors classes, because otherwise the better students would not be well served. They are absolutely correct, but there would not be such a difference if students had been allowed to take the class in an earlier year. When an algebra course is available for the best-prepared and most interested students at 7th grade, then it can reasonably be about the same course as that taught to other students at 8th and still others at 9th. But when you delay teaching algebra to these students even until 8th grade, the differences between these students and the 9th grade students are too great and the 8th grade needs to have much higher expectations.
In the last two years of high school, interest should begin to play a different role. Students then need to explore particular interests in beginning to think about what work they might do outside of school. We think the UCSMP six-year curriculum offers a coherent mathematics experience that exhibits the breadth of areas in which mathematics is applied while at the same time preparing students specifically for college-level courses in calculus, statistics, and discrete mathematics. But we know there is a transition time for many schools in which they have not started the UCSMP curriculum early enough, so they have students who are 10th graders who have completed UCSMP Advanced Algebra but who wish to take calculus as seniors. At that point, interest should be the key determiner whether a student takes FST and PDM, or a precalculus course and then calculus. This provides a viable choice for the student between the broad UCSMP curriculum that prepares for any college course, and a focussed curriculum that prepares only for calculus.
Individual Differences in Learning Style
Let me now turn to individual differences in the classroom, specifically, the differences in what is called learning style. What are these styles? We are told there are visual learners, oral learners, people who learn better in groups, people who must learn concretely. We know that there are actions that take place predominantly on one side of the brain or the other, though most thinking takes place in both sides at the same time, but this is translated into right-brain people and left-brain people.
Since there is righthandedness and lefthandedness, it is not so totally out of the question that there might be “rightbrainedness” and “leftbrainedness”. But we know that handedness is very much affected by experience — for example, every string musician, from guitar to violin, learns to do intricate maneuvers with the left hand even if righthanded in all other respects; every good pianist and basketball player learns to play with both hands rather well. And perhaps rightbrainedness and leftbrainedness are more like rightleggedness and leftleggedness, or righteyedness and lefteyedness. There may be a preference, but both sides work.
Learning style strikes me as a new phrase for a body of research a generation ago called aptitude-treatment interaction or ATI. Then, as now, the idea was that individuals learn in different ways, and the optimal pedagogy is one that takes advantage of these learning styles. ATI died because no one could determine a person’s particular learning style with any sort of reliability. The research showed that there were better pedagogies and worse pedagogies, and they worked independent of whatever style had been predicted. Thus it may be that in theory people have different learning styles, but in practice these cannot be pinned down. Or it may be that pedagogy is a far more powerful variable than learning style, so it cancels out the differences.
5. Individual differences in learning style are not able to be predicted with any certainty and do not warrant differences in instruction aimed at certain students, except in unusual circumstances such as learning disability.
Notice that this principle says “aimed at certain students”. Every teacher needs to accommodate the differences in learning style by aiming at classes, using different approaches to mathematical ideas. Some approaches are visual, some oral; some are deductive, some inductive; some utilize concrete materials or applications, others are symbolic. Because they are not able to be predicted, it is best to use and support student use of a variety of approaches to a particular topic. This is one of the main reasons for the SPUR approach to understanding, by which we approach virtually idea and look at its skills, properties, uses, and representations. A student may not at first understand the properties associated with a particular idea, but perhaps the uses or representations will lead the student to that point in the path through mathematics. At other times, the skills may be what comes first, and then the uses.
I am most troubled by the concept of learning style when I hear entire ethnic groups or races branded with one. Black mathematics educators have told me that African-Americans learn better concretely. Latinos have told me that Latinos learn better in groups. I have a book in my library called Women’s Ways of Knowing. I have great difficulty with such characterizations of entire groups of people as if they reflected natural attributes of those people. If these claims were made by nonmembers of the group, they might be branded as racist or sexist.
Differences in learning style thus strike me as a substitute for differences in ability, with about the same validity. Cultural stereotypes (such as that certain cultures learn best through concrete experiences while others do not) are vestiges of incorrect beliefs that students from some cultures do not possess the ability of students from others. The aptitude-treatment interaction research tells us that it is easier to predict which ideas are better learned concretely than which students learn better concretely, that some learn better in groups, and that there are men who have ways of knowing that are quite similar to the women’s ways. I just don’t know who they are.
Uri Treisman’s wonderful research with college freshmen at Berkeley found that his Oriental students were quite willing to cooperate on homework, while his Black students worked individually, much to the detriment of the Black students. But he was able to change the behavior of the Black students, and in doing so he brought their performance to be equal to their classmates. This indicates that different ethnic groups may behave differently because of social upbringing or social custom unless prodded to change behavior. Unless we are promoting behavior or learning styles that are against the ethics of a particular group, it seems to me that we should teach to a variety of learning styles in the classroom and promote each in the best light we can.
Individual Differences in Cultural Background
Learning style is, however, not the same as background. The backgrounds of students from different cultures are different. When we taught mathematics without contexts, as we tended to do until recent years, we did not have to consider the cultural backgrounds of students. What cultural background could possibly help a student to understand the division of polynomials? However, when one stresses the applicability of mathematics, differences must be taken into account in the learning experiences of students because context is such a critical variable in the learning. When the context is not understood, it is far more difficult to learn the concept. For instance, if we speak of the probability that a basketball player makes a free throw, it is an abstract problem to someone who does not know basketball, but a problem for which a basketball aficionado might know that the record for consecutive free throws in professional basketball is 97, set just this past week.
The teacher who teaches in a school where a significant number of students have Spanish as their first language is obviously better off with a knowledge of the Spanish language and the contributions of Spanish-speaking peoples to mathematics. When Jaime Escalante said to his students of Mexican ancestry in Stand and Deliver, referring to the contributions of the Maya, “It’s in your blood”, he was not saying something extraordinary, because mathematics is in all of our bloods, but his remarks had impact because he could cite examples. Increasingly the case in the United States, and more so as we expect all of our students to take the same mathematics, is the class where students come from a variety of ethnic and cultural backgrounds. If you teach such classes, you cannot be expected to have a knowledge of the origins and practices of mathematics worldwide, so in our second editions we are working to help you, with all sorts of information about how mathematics has developed and is used in other places in the world.
Arithmetic and geometry developed rather independently in cultures all over the world. But all cultures are not equal when it comes to today’s mathematics. Perhaps the best evidence that algebra is a language is that algebra has had a singular development. It originated with Diophantus and its transmission was aided by the Arabs, but it developed primarily in France and became immediately the language of mathematicians in Europe. The power of the language of algebra enabled the invention of analytic geometry and calculus by Frenchmen, an Englishmen, and a German within 100 years of its birth, and this western algebra is now used by mathematicians both pure and applied throughout the world.
We tend to group together the different cultures of those we do not know. There are a large number of cultures in Africa, many different cultures in India, many peoples included among the Arabs, many different strains of what we call Chinese, many more original peoples in Central and South America than the Mayas or Incas or Aztecs. For most cultures, the situation is the same as with the Jews. The culture developed some mathematical concepts. But the mathematics in use today was developed by others, even when developed geographically near them.
Even if today’s mathematics used by educated people throughout the world developed primarily in the west, it is important for instruction to accommodate different cultural backgrounds. In our second edition work we are trying to include a fair rendering of various cultures’ contributions to the development of the mathematics students are learning, while giving a taste of parallel mathematical ideas, as appropriate, that are applied or were developed in other cultures. We think that teachers and students should be able to choose from these contexts in their learning of mathematical ideas.
6. Individual differences in social, family and cultural background, even though great and diverse, are not enough to warrant differences in curriculum. But instruction needs to take into account these differences, because context is critical in the understanding of mathematics, the contributions of various cultures are important in conveying the universality of mathematical ideas, and because it helps students to develop a sense of ownership of these ideas.
Individual Differences in Teachers
I have come nearly to the end of my remarks. But there is another very important aspect of individual differences that I have thus far ignored. Almost every report that I have read about the teaching of mathematics also ignores this aspect. Teachers differ.
7. The same individual differences that apply to students also apply to teachers. Teachers differ in ability, entering knowledge, willingness to work, interests, teaching style, and background virtually as much as students do.
In the UCSMP materials, we assume teachers are equal in ability, but we know teachers differ in entering knowledge. That is why you find perspectives in our materials about the content of each book, chapter, and lesson, and comments on many problems. We cannot do much about your willingness to work except to provide you with material that is interesting enough so that you will want to see how it goes, and material that gives you and your students the feeling of success in reaching important objectives. We know you differ in teaching style and background — some of you love cooperative learning; others may seldom use it; some of you may love to work with computer programs, others of you merely tolerate them; some of you want to use manipulative materials, others of you may not. We also know you differ in cultural background, and so we try to give you information about what is in the materials that may be obvious to some but unknown to others.
Today and tomorrow you will hear of many ideas, given by a variety of people. We ask of you what you ask of your students. As teachers, our job is to change our students. And we know that the older the student is, the more difficult it is for the student to change. So it is more difficult for teachers to change. You have come here because you are changing what you are doing. If someone tells you of an idea that works for them, think of using it yourself. You have shown the interest and the willingness to work. For teachers as for students, these are the most important attributes to have. Our common goal has to be to organize mathematics experiences so that we nurture and maintain those attributes.
Contact
UCSMP
1427 East 60th Street
Chicago, IL 60637
T: 773-702-1130
F: 773-834-4665
ucsmp@uchicago.edu